题目内容
阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= 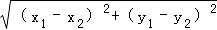 .
.
 例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=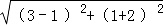 = .
= .
特别地,如果两 点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
【考点】勾股定理的逆定理;两点间的距离公式;勾股定理.
【专题】阅读型.
【分析】(1)根据两点间的距离公式即可求解;
(3)先根据两点间的距离公式求出 AB ,BC,AC 的长,再根据勾股定理的逆定理即可作出判断.
,BC,AC 的长,再根据勾股定理的逆定理即可作出判断.
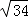 【解答】解:(1)AB=
【解答】解:(1)AB= = ;
= ;
AB=丨 5﹣(﹣1)丨=6;
(3)△ABC 是直角三角形
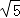 理由:∵AB=
理由:∵AB= 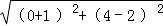 = ,BC=
= ,BC= 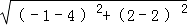 =5,
=5,
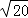 AC=
AC=  = ,
= ,
∴AB2+AC2=( 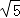 )2+(
)2+( 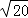 )2=25,BC2=52=25.
)2=25,BC2=52=25.
∴AB2+AC2=BC2
∴△ABC 是直角三角形.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长, 只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目


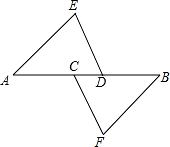
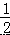 B.m<4C.
B.m<4C. 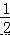 <m<4 D.m>4
<m<4 D.m>4
 +
+ 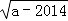 +3,其中 a 是实数,将式子 + 化简并求
+3,其中 a 是实数,将式子 + 化简并求 >
> ,
, ,那么
,那么 D.全等三角形对应角的平分线相等
D.全等三角形对应角的平分线相等