题目内容
在平面直角坐标系内点 A、点 B 的坐标分别为(0,3)、(4,3),在坐标轴上找一点 C,使△ABC
是等腰三角形,则符合条件的点 C 的个数是( )
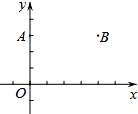
A.5 个 B.6 个 C.7 个 D.8 个
C【考点】等腰三角形的判定;坐标与图形性质.
【专题】分类讨论.
【分析】要使△ABC 是等腰三角形,可分三种情况(①若 AC=AB,②若 BC=BA,③若 CA=CB) 讨论,通过画图就可解决问题.
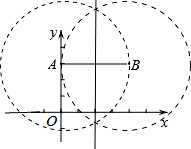
【解答】解:①若 AC=AB,则以点 A 为圆心,AB 为半径画圆,与坐标轴有 4 个交点;
②若 BC=BA,则以点 B 为圆心,BA 为半径画圆,与坐标轴有 2 个交点(A 点除外);
③若 CA=CB,则点 C 在 AB 的垂直平分线上,
∵A(0,3),B(4,3),
∴AB∥x 轴,
∴AB 的垂直平分线与坐标轴只有 1 个交点. 综上所述:符合条件的点 C 的个数有 7 个. 故选 C.
【点评】本题主要考查了等腰三角形的判定、圆的定义、垂直平分线的性质的逆定理等知识,还考 查了动手操作的能力,运用分类讨论的思想是解决本题的关键.

练习册系列答案
相关题目
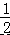 的倒数是
的倒数是  间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )
间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )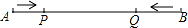
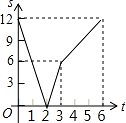
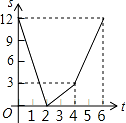 A.
A. 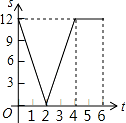 B.
B. 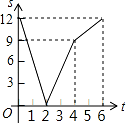 C.
C.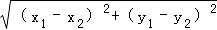 .
. 例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=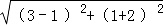 = .
= . 点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.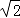 ,
, 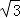 B.
B. 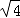 ,
,  C.6,8,10 D.5,12,13
C.6,8,10 D.5,12,13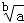 的值为
的值为 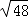

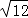
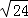 ÷ ﹣
÷ ﹣ 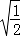 × + .
× + .