题目内容
 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长.
如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长.考点:相似三角形的判定与性质,圆周角定理
专题:
分析:利用条件可证明△CDE∽△CAD,再利用对应边成比例可求得AC,进一步可求得AE.
解答:解:∵AC平分∠BAD,
∴∠BAC=∠CAD=∠CDE,
且∠ACD=∠DCE,
∴△CDE∽△CAD,
∴
=
,即
=
,
解得CA=9,
∴AE=AC-CE=9-4=5.
∴∠BAC=∠CAD=∠CDE,
且∠ACD=∠DCE,
∴△CDE∽△CAD,
∴
| CE |
| CD |
| CD |
| CA |
| 4 |
| 6 |
| 6 |
| CA |
解得CA=9,
∴AE=AC-CE=9-4=5.
点评:本题主要考查相似三角形的判定和性质,利用条件证明△CDE∽△CAD从而利用对应边成比例求得AC的长是解题的关键.

练习册系列答案
相关题目
若
=7,则10y-2的值( )
| 5y-1 |
| 2 |
| A、14 | B、28 | C、30 | D、32 |
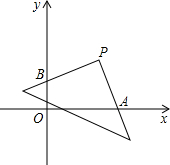 如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是
如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是