题目内容
20.两条直线被第三条直线所截,则( )| A. | 同位角不一定相等 | B. | 内错角必相等 | ||
| C. | 同旁内角必互补 | D. | 同位角定相等 |
分析 当两条互相平行的直线被第三条直线所截,截得的同位角相等,内错角相等,同旁内角互补,根据题意,两直线不平行,所B、C、D三项均不正确.
解答 解:∵两条被截的直线不平行,
∴截得的同位角不一定相等,内错角不一定相等,同旁内角不一定互补,
故选A.
点评 本题主要考查同位角,内错角,同旁内角的性质,平行线的性质,关键在于认真的阅读题目,熟练掌握相关的性质定理.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
8.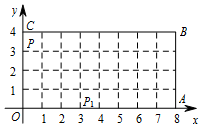 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( )
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,记点P第1次碰到矩形的边时的点为P1(3,0),第2次碰到长方形的边时的点为P2(7,4),以此类推,则点P2014的坐标为( )| A. | (1,4) | B. | (6,4) | C. | (5,0) | D. | (8,3) |
9.下列能断定△ABC为等腰三角形的是( )
| A. | ∠A=30°,∠B=60° | B. | ∠A=50°,∠B=80° | ||
| C. | ∠A=2∠B=80° | D. | AB=3,BC=6,周长为13 |
10.甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( )
| A. | $\left\{\begin{array}{l}6x=5y\\ x=2y-40\end{array}\right.$ | B. | $\left\{\begin{array}{l}6x=5y\\ x=2y+40\end{array}\right.$ | C. | $\left\{\begin{array}{l}5x=6y\\ x=2y+40\end{array}\right.$ | D. | $\left\{\begin{array}{l}5x=6y\\ x=2y-40\end{array}\right.$ |
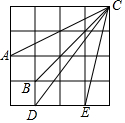 如图,图中是16个边长为1的小正方形拼成的大正方形,连接CA,CB,CD,CE四条线段,其中长度既不是整数也不是分数的有3条.
如图,图中是16个边长为1的小正方形拼成的大正方形,连接CA,CB,CD,CE四条线段,其中长度既不是整数也不是分数的有3条. 在△ABC中,AD是中线,已知△ADC的周长比△ABD的周长多5cm,AB长为3cm.求AC的长.
在△ABC中,AD是中线,已知△ADC的周长比△ABD的周长多5cm,AB长为3cm.求AC的长. 如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点E,边结CE、DE
如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点E,边结CE、DE