题目内容
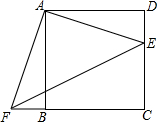 如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.(1)试判断△AEF的形状,并说明理由;
(2)若DE=1,求△AFE的面积.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)正方形的边长相等,四个角相等,即AD=AB,∠ABF=∠D=90°,根据条件还能证∠FAB=∠DAE,故能证明△ADE≌△ABF,进而得出AE=AF即可得出答案;
(2)利用DE=1,AD=4,根据勾股定理能求出AE的长,进而得出答案.
(2)利用DE=1,AD=4,根据勾股定理能求出AE的长,进而得出答案.
解答:解:(1)△AEF是等腰直角三角形,
理由:∵AF⊥AE,
∴∠FAB+∠EAB=90°,
∵∠DAE+∠EAB=90°,
∴∠FAB=∠DAE,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(ASA),
∴AF=AE,
又∵AF⊥AE,
∴△AEF是等腰直角三角形;
(2)∵DE=1,AD=4,∠D=90°,
∴AE=
=
.
∴△AFE的面积为:
×
×
=
.
理由:∵AF⊥AE,
∴∠FAB+∠EAB=90°,
∵∠DAE+∠EAB=90°,
∴∠FAB=∠DAE,
在△ADE和△ABF中,
|
∴△ADE≌△ABF(ASA),
∴AF=AE,
又∵AF⊥AE,
∴△AEF是等腰直角三角形;
(2)∵DE=1,AD=4,∠D=90°,
∴AE=
| 12+42 |
| 17 |
∴△AFE的面积为:
| 1 |
| 2 |
| 17 |
| 17 |
| 17 |
| 2 |
点评:本题考查了正方形的性质以及全等三角形的判定和性质,得出△ADE≌△ABF是解题关键.

练习册系列答案
相关题目
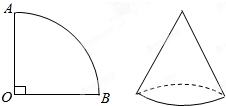 如图,已知扇形OAB的圆心角为90°,半径为4厘米,用这个扇形卷成的圆锥的侧面,求该圆锥圆锥的侧面积及圆锥的高.
如图,已知扇形OAB的圆心角为90°,半径为4厘米,用这个扇形卷成的圆锥的侧面,求该圆锥圆锥的侧面积及圆锥的高.