题目内容
解方程
（1）x2+5x+7=3x+11
（2）x（2x-5）=4x-10．
（1）x2+5x+7=3x+11
（2）x（2x-5）=4x-10．
考点：解一元二次方程-因式分解法,解一元二次方程-配方法
专题：
分析：（1）方程化简后用配方法解答；
（2）方程化为一般形式，用公式法解答．
（2）方程化为一般形式，用公式法解答．
解答：解：（1）方程可化为x2+2x=4，
配方得x2+2x+1=5，
（x+1）2=5，
开方得x+1=±
，
x1=-1+
，x2=-1-
．
（2）方程可化为2x2-9x+10=0，
a=2，b=-9，c=10，
△=81-4×2×10=1，
x=
，
x1=
，x2=2．
配方得x2+2x+1=5，
（x+1）2=5，
开方得x+1=±
| 5 |
x1=-1+
| 5 |
| 5 |
（2）方程可化为2x2-9x+10=0，
a=2，b=-9，c=10，
△=81-4×2×10=1，
x=
| 9±1 |
| 4 |
x1=
| 5 |
| 2 |
点评：本题考查了一元二次方程的解法，要会利用适当的方法解答不同的方程．
练习册系列答案
计算高手系列答案
相关题目
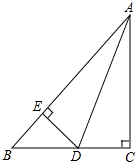已知，如图，AD平分∠BAC，∠C=90°，DE⊥AB，那么：
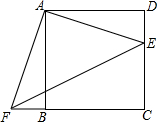如图，正方形ABCDE的边长为4，E是正方形ABCD的边DC上的一点，过A作AF⊥AE，交CB延长线于点F．