题目内容
如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
C
考点: 作图—基本作图.
分析: 根据角平分线的做法可得①正确,再根据直角三角形的高的定义可得②正确,然后计算出∠CAD=∠DAB=29°,可得AD≠BD,根据到线段两端点距离相等的点在线段的垂直平分线上,因此③错误,根据三角形内角和可得④正确.
解答: 解:根据作法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,
∴CD是△ADC的高,故②正确;
∵∠C=90°,∠B=32°,
∴∠CAB=58°,
∵AD是∠BAC的平分线,
∴∠CAD=∠DAB=29°,
∴AD≠BD,
∴点D不在AB的垂直平分线上,故③错误;
∵∠CAD=29°,∠C=90°,
∴∠CDA=61°,故④正确;
共有3个正确,
故选:C.
点评: 此题主要考查了基本作图,关键是掌握角平分线的做法和线段垂直平分线的判定定理.

练习册系列答案
相关题目
 ﹣
﹣ +
+ ﹣
﹣ )×(﹣4.8)
)×(﹣4.8)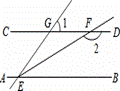
 海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.
海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.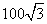 海里范围内有暗礁.若巡逻船C沿直线CF去营救船F,在去营救的途中有无触暗礁危险?(参考数据:
海里范围内有暗礁.若巡逻船C沿直线CF去营救船F,在去营救的途中有无触暗礁危险?(参考数据: ,
,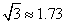 ,
, )
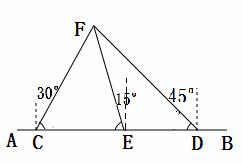
)
 ]=1,现对72进行如下操作:72→[
]=1,现对72进行如下操作:72→[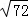 ]=8→[
]=8→[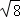 ]=2→[
]=2→[ ]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )
]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )
 的图象上的两点,若x1<0<x2,则y1 y2.
的图象上的两点,若x1<0<x2,则y1 y2. 和点
和点 ,如果
,如果 ,那么 ( )
,那么 ( ) B.点
B.点