Question

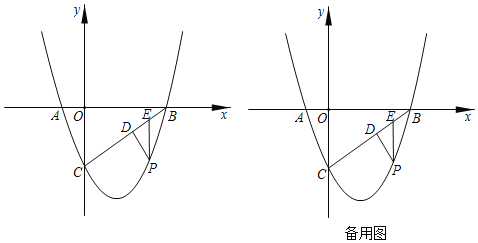
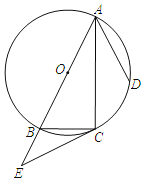
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D在⊙O上，AC平分∠BAD，延长AB到点E且有∠BCE＝∠CAD．

（1）求证：CE是⊙O的切线；

（2）若AB＝10，AD＝6，求BC，CE的长．

Answer 1

【答案】（1）见解析；（2），

【解析】

（1）连接OC，根据等腰三角形的性质得到∠1＝∠2，根据圆周角定理得到∠ACB＝90°，根据角平分线的定义得到∠3＝∠CAD，求得CE⊥OC，于是得到结论；

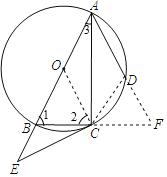
（2）连接CD，分别延长AD、BC相交于点F．根据三角形的内角得到∠3＝∠CAD，根据相似三角形的性质得到，设BC＝x，求得，根据相似三角形的性质即可得到结论．

（1）证明：连接OC，

∵在⊙O中OB＝OC，

∴∠1＝∠2，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∵AC平分∠BAD，

∴∠3＝∠CAD，

∵∠BCE＝∠CAD，

∴∠3＝∠CAD，

∴∠OCE＝∠BCE+∠2＝∠3+∠1＝90°，

∴CE⊥OC，

∴CE是⊙O的切线；

（2）解：连接CD，分别延长AD、BC相交于点F．

在Rt△ACB中，∠1＝90°﹣∠3，

在Rt△ACF中，∠F＝90°﹣∠CAD，

又∵∠3＝∠CAD，

∴∠1＝∠F，

∴在△ABF中，AB＝AF，

∴BC＝CF，

∵在⊙O中∠3＝∠CAD，

∴BC＝CD，

∴CD＝CF，

∴在△CDF中，∠CDF＝∠F，

∴∠1＝∠CDF，

又∵∠F＝∠F，

∴△CDF∽△ABF，

∴，

设BC＝x，则有，

∴，

即，

在Rt△ACB中，，

∵在△BEC和△DAC中，∠BCE＝∠CAD，∠EBC＝∠ADC，

∴△BEC∽△DCA，

∴，

则，

∴．