题目内容
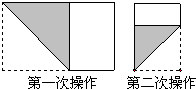长为2，宽为a的矩形纸片（1＜a＜2），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为考点：翻折变换（折叠问题）
专题：
分析：根据操作步骤，可知每一次操作时所得正方形的边长都等于原矩形的宽．所以首先需要判断矩形相邻的两边中，哪一条边是矩形的宽．当1＜a＜2时，矩形的长为2，宽为a，所以第一次操作时所得正方形的边长为a，剩下的矩形相邻的两边分别为2-a，a．由2-a＜a可知，第二次操作时所得正方形的边长为2-a，剩下的矩形相邻的两边分别为2-a，a-（2-a）=2a-2．由于（2-a）-（2a-2）=4-3a，所以（2-a）与（2a-2）的大小关系不能确定，需要分情况进行讨论．又因为可以进行三次操作，故分两种情况：①2-a＞2a-2；②2-a＜2a-2．对于每一种情况，分别求出操作后剩下的矩形的两边，根据剩下的矩形为正方形，列出方程，求出a的值．
解答：解：由图可知，第一次操作后剩下的矩形长为：原矩形的长-原矩形的宽，即为：2-a
∵第二次操作后剩下的矩形的边长分别为：2-a，2a-2，
∴面积为：（2-a）（2a-2）=-2a2+6a-4，
②当2-a＞2a-2，a＜
时，2-a=2（2a-2），
解得：a=
；
当2-a＜2a-2，a＞
时，2（2-a）=2a-2，
解得：a=
；
综合得a=
或
．
故答案为：a=
或
．
∵第二次操作后剩下的矩形的边长分别为：2-a，2a-2，
∴面积为：（2-a）（2a-2）=-2a2+6a-4，
②当2-a＞2a-2，a＜
| 4 |
| 3 |
解得：a=
| 6 |
| 5 |
当2-a＜2a-2，a＞
| 4 |
| 3 |
解得：a=
| 3 |
| 2 |
综合得a=
| 6 |
| 5 |
| 3 |
| 2 |
故答案为：a=
| 6 |
| 5 |
| 3 |
| 2 |
点评：本题考查了翻折的性质，矩形的性质和正方形的性质以及正方形、矩形的面积公式以及分类讨论思想在几何题目中的运用．
练习册系列答案
相关题目
蜡烛燃烧时余下的长度y（cm） 和燃烧的时间x（分钟）的关系如图．