题目内容
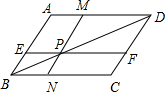如图四边形ABCD中EF∥AD，MN∥AB，MN与EF交于点P且点P在BD上，图中面积相等的四边形有考点：平行四边形的判定与性质
专题：几何图形问题
分析：根据平行四边形的性质可得，S△ABD=S△DBC，S△BEP=S△BNP，S△MPD=S△DPF，根据三角形的面积相等，推出平行四边形的面积相等，即S?AEPM=S?PNCF，从而得到S?ABMN=S?EBCF，同理，S?AEFD=S?CDMN，S四边形ABPG=S四边形CBPF；S四边形ADPE=S四边形CDPN．
解答：解：∵在平行四边形ABCD中，BD是对角线，EF∥BC，GN∥AB，
∴S△ABD=S△DBC，S△BEP=S△BNP，S△MPD=S△DPF，
∴S△ABD-S△BEP-S△MPD=S△DBC-S△BNP-S△DPF，
∴S?AEPM=S?PNCF，
∴S?AEPM+S?EBHP=S?PNCF+S?EBNP，
即，S?ABMN=S?EBCF，
同理，S?AEFD=S?CDMN，
S四边形ABPM=S四边形CBPF；S四边形ADPE=S四边形CDPN
∴图中有5对四边形面积相等，即：S?AEPM=S?PNCF，S?ABNM=S?EBCF，S?AEFD=S?CDMN，S四边形ABPM=S四边形CBPF；S四边形ADPE=S四边形CDPN
故答案是：5．
∴S△ABD=S△DBC，S△BEP=S△BNP，S△MPD=S△DPF，
∴S△ABD-S△BEP-S△MPD=S△DBC-S△BNP-S△DPF，
∴S?AEPM=S?PNCF，
∴S?AEPM+S?EBHP=S?PNCF+S?EBNP，
即，S?ABMN=S?EBCF，
同理，S?AEFD=S?CDMN，
S四边形ABPM=S四边形CBPF；S四边形ADPE=S四边形CDPN
∴图中有5对四边形面积相等，即：S?AEPM=S?PNCF，S?ABNM=S?EBCF，S?AEFD=S?CDMN，S四边形ABPM=S四边形CBPF；S四边形ADPE=S四边形CDPN
故答案是：5．
点评：本题主要考查了平行四边形的性质，解答本题的关键，是掌握平行四边形被一条对角线分成的两个三角形的面积相等，使学生能够灵活运用平行四边形的知识解决有关问题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
在梯形ABCD中，AD∥BC，∠B=90°，AB=12，BC=10，AD=5，则CD的长是（ ）
| A、13 | B、14 | C、15 | D、16 |
在4×4方格内画三角形ABC，使它的顶点在格点上，三条边长分别为2，2