题目内容
函数y=2
+
的最大值为 .
| a-1 |
| 2-a |
考点:无理函数的最值
专题:计算题
分析:由二次根式的性质可得1≤a≤2,然后由柯西不等式求得y=2
+
≤
•
=
×
=
.
| a-1 |
| 2-a |
| 12+22 |
(
|
| 5 |
| a-1+2-a |
| 5 |
解答:解:根据题意得:
,
解得:1≤a≤2,
由柯西不等式得:y=2
+
≤
•
=
×
=
,(当且仅当2
=
,即a=
时,取等号);
∴函数y=2
+
的最大值为:
.
故答案为:
.
|
解得:1≤a≤2,
由柯西不等式得:y=2
| a-1 |
| 2-a |
| 12+22 |
(
|
| 5 |
| a-1+2-a |
| 5 |
| 2-a |
| a-1 |
| 9 |
| 5 |
∴函数y=2
| a-1 |
| 2-a |
| 5 |
故答案为:
| 5 |
点评:此题考查了无理函数的最值问题.此题难度适中,注意掌握柯西不等式的应用是解此题的关键,注意柯西不等式:ax+by≤
•
(当且仅当ay=bx时取“=”).
| a2+b2 |
| x2+y2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
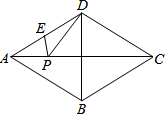 已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是
已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是 如图,AC、BD是相交的两条线段,O分别为它们的中点.当BD绕点O旋转时,连接AB、BC、CD、DA所得到的四边形ABCD始终为
如图,AC、BD是相交的两条线段,O分别为它们的中点.当BD绕点O旋转时,连接AB、BC、CD、DA所得到的四边形ABCD始终为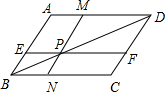 如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有
如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有 如图,点A,C和B都在⊙O上,且四边形ACBO为菱形,求证:点C是
如图,点A,C和B都在⊙O上,且四边形ACBO为菱形,求证:点C是