题目内容
在梯形ABCD中,AD∥BC,∠B=90°,AB=12,BC=10,AD=5,则CD的长是( )
| A、13 | B、14 | C、15 | D、16 |
考点:梯形
专题:计算题
分析:过点D作DE⊥BC于点E,易证四边形ABDE是矩形,所以BE和DE长可求,进而求出CE的长,再利用勾股定理即可求出CD的长.
解答:解:过点D作DE⊥BC于点E,

∵∠B=90°
∴四边形ABDE是矩形,
∴BE=AD=5,DE=AB=12,
∴CE=10-5=5,
CD=
=13.
故选A.

∵∠B=90°
∴四边形ABDE是矩形,
∴BE=AD=5,DE=AB=12,
∴CE=10-5=5,
CD=
| CE2+DE2 |
故选A.
点评:本题考查梯形及勾股定理的知识,注意:直角梯形中常见的辅助线是作另一高.可以构造一个矩形和一个直角三角形,根据它们的性质进行分析计算.

练习册系列答案
相关题目
为了调查全省中学生吃早餐的情况,采用抽样调查方式,在下列抽样方法中,最合理的是( )
| A、抽取几个乡镇的中学生 |
| B、抽取几所城市学校中学生 |
| C、抽取一个地方的所有中学生 |
| D、从每个地方各抽取几个学校的中学生 |
某同学在解方程3x-1=□x+2时,把□处的数字看错了,解得x=-1,则该同学把□看成了( )
| A、3 | ||
B、
| ||
| C、6 | ||
D、-
|
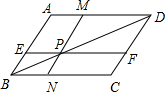 如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有
如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有 如图,点A,C和B都在⊙O上,且四边形ACBO为菱形,求证:点C是
如图,点A,C和B都在⊙O上,且四边形ACBO为菱形,求证:点C是
 如图,在?ABCD中,若BE平分∠ABC,求ED.
如图,在?ABCD中,若BE平分∠ABC,求ED.