题目内容
16．
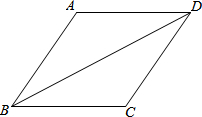如图，四边形ABCD中，CD=3，BD=2$\sqrt{6}$，sin∠DBC=$\frac{\sqrt{3}}{3}$，求BC的长．
分析 过D作DE⊥BC，角BC的延长线于E，解直角三角形即可得到结论．
解答 
解：过D作DE⊥BC，角BC的延长线于E，
在Rt△BED中，
∵DE=BD•sin∠DBC=2$\sqrt{2}$，
∴BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{（2\sqrt{6}）^{2}-（2\sqrt{2}）^{2}}$=4，
CE=$\sqrt{C{D}^{2}-D{E}^{2}}$=$\sqrt{{3}^{2}-（2\sqrt{2}）^{2}}$=1，
∴BC=BE-CE=3．
点评 本题考查了解直角三角形，正确的作出辅助线构造直角三角形是解题的关键．
练习册系列答案
相关题目
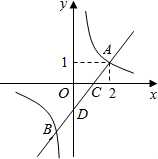如图，一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1）．
Rt△ABC中，∠BAC=90°，AB=AC，∠DAE=45°，将△BAD绕点A逆时针旋转与△CAF重合，BD=1，DE=3，则EC=2$\sqrt{2}$．
如图，反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=$\frac{1}{4}$x的图象交于点A、B，点B的横坐标是4，点P（1，m）在反比例函数y1=$\frac{k}{x}$的图象上．
1．下列方程中，是二元一次方程的是（ ）
| A． | 2x2-3y=12 | B． | 4x-4y=7 | C． | $\frac{1}{x}$-y-2=0 | D． | x-y+xy=6 |