题目内容
4.计算或化简:(1)计算:2-1+$\sqrt{3}$cos30°+|-5|-(π-2017)0
(2)化简:(x-5+$\frac{16}{x+3}$)÷$\frac{x-1}{{x}^{2}-9}$.
分析 (1)根据负整数指数幂、特殊角的三角函数值、绝对值、零指数幂可以解答本题;
(2)根据分式的加法和除法可以解答本题.
解答 解:(1)2-1+$\sqrt{3}$cos30°+|-5|-(π-2017)0
=$\frac{1}{2}+\sqrt{3}×\frac{\sqrt{3}}{2}+5-1$
=$\frac{1}{2}+\frac{1}{2}+5-1$
=5;
(2)(x-5+$\frac{16}{x+3}$)÷$\frac{x-1}{{x}^{2}-9}$
=$\frac{(x-5)(x+3)+16}{x+3}•\frac{(x+3)(x-3)}{x-1}$
=$\frac{(x-1)^{2}}{x+3}•\frac{(x+3)(x-3)}{x-1}$
=(x-1)(x+3)
=x2+2x-3.
点评 本题考查分式的混合运算、实数的运算、负整数指数幂、特殊角的三角函数值、绝对值、零指数幂,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.科学家在实验中检测出某微生物细胞直径约为0.0000035米,将0.0000035用科学记数法表示为( )
| A. | 3.5×1 0-6 | B. | 3.5×1 06 | C. | 3.5×1 0-5 | D. | 35×1 0-5 |
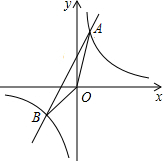 已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(1,8),B(-4,m),
已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(1,8),B(-4,m),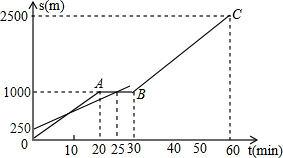 小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
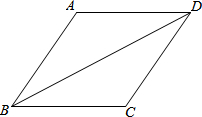 如图,四边形ABCD中,CD=3,BD=2$\sqrt{6}$,sin∠DBC=$\frac{\sqrt{3}}{3}$,求BC的长.
如图,四边形ABCD中,CD=3,BD=2$\sqrt{6}$,sin∠DBC=$\frac{\sqrt{3}}{3}$,求BC的长.