题目内容
2. 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.
(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
分析 (1)把A(-1,0),C(0,5),(1,8)三点代入二次函数解析式,解方程组即可.
(2)先求出M、B、C的坐标,根据S△MCB=S梯形MEOB-S△MCE-S△OBC即可解决问题.
(3)分三种情①C为直角顶点;②B为直角顶点;③N为直角顶点;分别求解即可.
解答 解:(1)∵二次函数y=ax2+bx+c的图象经过A(-1,0),C(0,5),(1,8),
则有:$\left\{\begin{array}{l}{a-b+c=0}\\{a+b+c=8}\\{c=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=5}\end{array}\right.$.
∴抛物线的解析式为y=-x2+4x+5.
(2)令y=0,得(x-5)(x+1)=0,x1=5,x2=-1,
∴B(5,0).
由y=-x2+4x+5=-(x-2)2+9,得顶点M(2,9)
如图1中,作ME⊥y轴于点E,
可得S△MCB=S梯形MEOB-S△MCE-S△OBC=$\frac{1}{2}$(2+5)×9-$\frac{1}{2}$×4×2-$\frac{1}{2}$×5×5=15.
(3)存在.如图2中,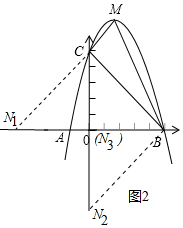
∵OC=OB=5,
∴△BOC是等腰直角三角形,
①当C为直角顶点时,N1(-5,0).
②当B为直角顶点时,N2(0,-5).
③当N为直角顶点时,N3(0,0).
综上所述,满足条件的点N坐标为(0,0)或(0,-5)或(-5,0).
点评 本题考查二次函数综合题、三角形的面积、直角三角形的判定和性质等知识,解题的关键是学会利用分割法求面积,学会分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
13.能使分式方程$\frac{k}{1-x}$+2=$\frac{3}{x-1}$有非负实数解且使一次函数y=(k+2)x-1的图象不经过第一象限的所有整数k的积为( )
| A. | 20 | B. | -20 | C. | 60 | D. | -60 |
10.九年级数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价y(单位:元/件)与时间x(单位:天)的函数关系式为y=$\left\{\begin{array}{l}{x+40(0≤x≤50,且x为整数)}\\{90(50<x≤90,且x为整数)}\end{array}\right.$;在第x天的销售量p(单位:件)与时间x(单位:天)的函数关系的相关信息如表.已知商品的进价为30元/件,每天的销售利润为w(单位:元).
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
17.下列运算中,结果最小的是( )
| A. | -(-3-2)2 | B. | (-3)×(-2) | C. | (-3)2÷(-2)2 | D. | -32÷-2 |
14. 如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
 如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
11.一元二次方程3x2-5x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |