题目内容
16. 如图,已知A、B、C分别是⊙O上的点,∠B=120°,P是直径CD的延长线上的一点,且AP=AC,PD=2,求AP的长为2$\sqrt{3}$.
如图,已知A、B、C分别是⊙O上的点,∠B=120°,P是直径CD的延长线上的一点,且AP=AC,PD=2,求AP的长为2$\sqrt{3}$.
分析 连接AD、OA,根据圆内接四边形的性质得到∠ADC=60°,根据等腰三角形的性质得到AD=PD=2,根据切线的判定定理得到PA是⊙O的切线,根据切割线定理计算得到答案.
解答 解:连接AD、OA,
∵∠B=120°,∴∠ADC=60°,
∴∠ACD=30°,又AP=AC,
∴∠P=30°,∠DAP=30°,
∴AD=PD=2,则CD=4,
∵OA=OD,∴∠OAD=∠ADC=60°,
∴∠OAP=90°,
∴PA是⊙O的切线,
∴PA2=PD•PC=12,
则AP=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查的是圆周角定理、圆内接四边形的性质和直角三角形的性质,掌握直角所对的圆周角是直角、圆内接四边形对角互补是解题的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
6.已知双曲线y=$\frac{k-1}{x}$过点A(1,1),那么过点A的直线y=kx+b经过( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
7.若点A(x1,1)、B(x2,2)、C(x3,-3)在双曲线y=-$\frac{1}{x}$上,则( )
| A. | x1>x2>x3 | B. | x1>x3>x2 | C. | x3>x2>x1 | D. | x3>x1>x2 |

 如图,
如图,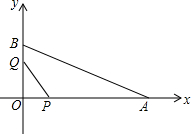 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1厘米/秒的速度移动,点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6),那么
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1厘米/秒的速度移动,点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6),那么