Question

7．如图，在直线l上依次摆放着三个边长分别为1、2、3的等边三角形：△ABC，△HFG，△DCE，点F是BC的中点，FM∥AC，GN∥DC，设图中三个平行四边形的面积依次为S₁，S₂，S₃，则S₂=$\frac{3\sqrt{3}}{8}$．

Answer 1

分析 根据正三角形的性质，∠ABC=∠HFG=∠DCE=60°，根据AB∥HF∥DC∥GN，设AC与FH交于P，CD与HG交于Q于是得到△PFC、△QCG和△NGE是正三角形，由F是BC的中点，推出CF=$\frac{1}{2}$，CG=$\frac{3}{2}$，于是得到CQ=CG=$\frac{3}{2}$，通过△GQC∽△GHF，求出S_△GQC=$\frac{9\sqrt{3}}{16}$，由于S_△CPF=$\frac{1}{4}$S_△ABC=$\frac{\sqrt{3}}{16}$，于是得到结论．

解答 解：根据正三角形的性质，∠ABC=∠HFG=∠DCE=60°，
∴AB∥HF∥DC∥GN，
设AC与FH交于P，CD与HG交于Q
∴△PFC、△QCG和△NGE是正三角形，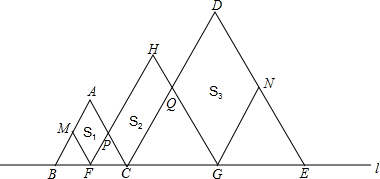
∵F是BC的中点，
∴CF=$\frac{1}{2}$，∵FG=2，
∴CG=$\frac{3}{2}$，
∴CQ=CG=$\frac{3}{2}$，
∵CQ∥HF，
∴△GQC∽△GHF，
∴$\frac{{S}_{△GQC}}{S△GHF}$=$\frac{9}{16}$，
∵S_△HFG=$\frac{1}{2}×$2×$\sqrt{3}$=$\sqrt{3}$，
∴S_△GQC=$\frac{9\sqrt{3}}{16}$，
∵S_△CPF=$\frac{1}{4}$S_△ABC=$\frac{\sqrt{3}}{16}$，
∴S₂=S_△GHF-S_△GQC-S_△CPF=$\frac{3\sqrt{3}}{8}$．
故答案为：$\frac{3\sqrt{3}}{8}$．

点评 此题主要考查了面积及等积变换、等边三角形的性质及平行四边形的面积求法，平行四边形的面积等于平行四边形的边长与该边上的高的积．即S=a•h．其中a可以是平行四边形的任何一边，h必须是a边与其对边的距离，即对应的高．