题目内容
17.解方程(组):(1)2-$\frac{2x+1}{3}$=$\frac{1+x}{2}$
(2)$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$.
分析 (1)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
(2)将第二个方程乘以6去掉分母,然后利用加减消元法解二元一次方程组即可.
解答 解:(1)去分母得,12-2(2x+1)=3(1+x),
去括号得,12-4x-2=3+3x,
移项得,-4x-3x=3-12+2,
合并同类项得,-7x=-7,
系数化为1得,x=1;
(2)$\left\{\begin{array}{l}{3x-5y=3①}\\{\frac{x}{2}-\frac{y}{3}=1②}\end{array}\right.$,
②×6得,3x-2y=6③,
③-①得,3y=3,
解得y=1,
将y=1代入①得,3x-5=3,
解得x=$\frac{8}{3}$,
所以,方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=1}\end{array}\right.$.
点评 本题考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
相关题目
6.下列关系正确的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a-b)2=a2-2ab-b2 |
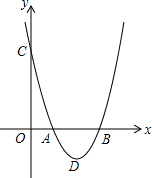 如图,二次函数y=a(x2-4x+3)(a>0)的图象与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点
如图,二次函数y=a(x2-4x+3)(a>0)的图象与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点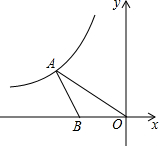 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$.
如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$. 已知:如图,在平面直角坐标系xOy中,直线y=$\frac{4}{3}$x+4与x轴交于A、与y轴交于 B,点C(a,b),其中a<b,且a、b是方程x2-7x+12=0的两根.
已知:如图,在平面直角坐标系xOy中,直线y=$\frac{4}{3}$x+4与x轴交于A、与y轴交于 B,点C(a,b),其中a<b,且a、b是方程x2-7x+12=0的两根.