Question

5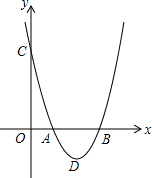．如图，二次函数y=a（x²-4x+3）（a＞0）的图象与x轴交于A、B两点，与y轴交于点C，点D是抛物线的顶点
（1）若△ABD为直角三角形，求此二次函数的解析式；
（2）P为抛物线对称轴上一点，且P点的纵坐标t是大于3的常数，试问是否存在一个正数a，使得四边形PA、PB、PC、PD与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）？请说明理由．
（3）是否存在实数a，使得△OAC沿AC翻折后，点O的对应点O′落在△ABC的外部？若存在，求出a的范围，若不存在，请说明理由．

Answer 1

分析 （1）求出A、B、D坐标，理由等腰直角三角形性质即可解决问题．
（2）存在．先求出直线CD解析式，再求出线段CD的垂直平分线的解析式，即可求出点P坐标，观察点P纵坐标即可解决问题．
（3）存在．如图2中，作AF⊥BC，垂足为F，求出OA=AF时，OC的长即可解决问题．

解答 解：（1）令y=0，则x²-4x+3=0，
解得x=3或1，
∴A（1，0）．B（3，0），
又∵y=a（x-2）²-a，
∴顶点D（2，-a），
∵△ABD是直角三角形，DA=DB，
∴|-a|=$\frac{1}{2}$AB，
|-a|=1，
∵a＞0，
∴a=1，
∴二次函数解析式为y=x²-4x+3，
（2）存在．
理由：如图1中，∵点P在对称轴上，
∴PA=PB，
∵四边形PA、PB、PC、PD与一个平行四边形的四条边对应相等，
∴PC=PD，设点P（2，t），
∵C（0，3a），D（2，-a），
∴直线CD解析式为y=-2ax+3a，线段CD的垂直平分线的解析式为y=$\frac{1}{2a}$x+a-$\frac{1}{2a}$，
∴点P的纵坐标t=$\frac{1}{2a}$+a，
∴当a=3时，t＞3，
∴存在一个正数a，使得四边形PA、PB、PC、PD与一个平行四边形的四条边对应相等．
（3）如图2中，作AF⊥BC，垂足为F，
当OA=AF=1时，在RT△AFB中，∵AB=2，AF=1，
∴AB=2AF，
∴∠ABF=30°，
∴在RT△BOC中，∵∠BOC=90°，∠OBC=30°，OB=3，
∴OC=OB•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$，
由图象可知当0＜3a＜$\sqrt{3}$时，即0＜a$＜\frac{\sqrt{3}}{3}$时，点O的对应点O′落在△ABC的外部．

点评 本题考查二次函数综合题、平行四边形的性质、翻折变换，直角三角形30度角所对的直角边等于斜边的一半等知识，解题的关键是构建一次函数求出点P坐标，学会添加常用辅助线，第三个问题的关键是求出AF=OA时OC的长，属于中考压轴题．