题目内容
17．若直角三角形的两直角边各扩大1倍，则斜边扩大（ ）| A． | 3倍 | B． | 1倍 | C． | 2倍 | D． | 4倍 |
分析 设直角三角形ABC的三边长为a、b、c，c为斜边，由勾股定理得c=$\sqrt{{a}^{2}+{b}^{2}}$，$\sqrt{（2a）^{2}+（2b）^{2}}$=2c；2c-c=c，即可得出结果．
解答 解：设直角三角形ABC的三边长为a、b、c，c为斜边，
则c=$\sqrt{{a}^{2}+{b}^{2}}$；
直角三角形ABC的两直角边各扩大1倍后，两直角边长为2a、2b，
则$\sqrt{（2a）^{2}+（2b）^{2}}$=2$\sqrt{{a}^{2}+{b}^{2}}$=2c；
2c-c=c．
故选：B．
点评 本题考查了勾股定理；熟练掌握勾股定理，由勾股定理求出扩大后的斜边长是解决问题的关键．
练习册系列答案
53随堂测系列答案
相关题目
7．若-$\frac{3}{x}$＞-$\frac{2}{x}$，则x的取值范围为（ ）
| A． | x＞0 | B． | x＜0 | C． | x是整数 | D． | -1＜x＜0 |
5．点P在第二象限内，P到x轴的距离是5，到y轴的距离是3，那么点P的坐标为（ ）
| A． | （-5，3） | B． | （-3，-5） | C． | （-3，5） | D． | （3，-5） |
细心观察所示图形，认真分析各式，然后解答问题．
9．式子4×25×（$\frac{1}{2}$-$\frac{3}{10}$+$\frac{2}{5}$）=100（$\frac{1}{2}$-$\frac{3}{10}$+$\frac{2}{5}$）=50-30+40中用的运算律是（ ）
| A． | 乘法交换律及乘法结合律 | B． | 乘法交换律及分配律 | ||
| C． | 乘法结合律及分配律 | D． | 分配律及加法结合律 |
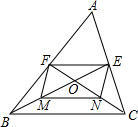在△ABC中，中线BE、CF交于点O，M、N分别是BO、CO中点，则四边形MNEF是什么特殊四边形？并说明理由．