题目内容
5．已知代数式x+2y的值是4，则代数式2x+4y+1的值是（ ）| A． | 4 | B． | 6 | C． | 9 | D． | 不能确定 |
分析 把x+2y=4代入代数式2x+4y+1，求出算式的值是多少即可．
解答 解：∵x+2y=4，
∴2x+4y+1
=2（x+2y）+1
=2×4+1
=8+1
=9
故选：C．
点评 此题主要考查了代数式求值问题，要熟练掌握，求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．题型简单总结以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简．
练习册系列答案
相关题目
15．2016年12月16日央视新闻报道：“不施肥不打药，袁隆平用海水种出红色水稻-海稻86”．其科研组在研究过程中，将“海稻86”在不同条件的甲、乙两块试验田进行试验，得到每块试验田每亩产量的两组数据，其方差分别为s2甲=0.002，s2乙=0.03，则（ ）
| A． | 甲比乙的产量稳定 | B． | 乙比甲的产量稳定 | ||
| C． | 甲、乙的产量一样稳定 | D． | 无法确定哪一品种的产量更稳定 |
10．下列图形都是由同样大小的⊙按一定规律所组成的，其中第1个图形中一共有5个⊙，第2个图形中一共有8个⊙，第3个图形中一共有11个⊙，第4个图形中一共有14个⊙，…，按此规律排列，第1001个图形中基本图形的个数为（ ）
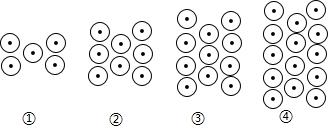
| A． | 2998 | B． | 3001 | C． | 3002 | D． | 3005 |
14．阅读下列材料：
有这样一个问题：关于x 的一元二次方程a x2+bx+c=0（a＞0）有两个不相等的且非零的实数根．探究a，b，c满足的条件．
小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：
①设一元二次方程ax2+bx+c=0（a＞0）对应的二次函数为y=ax2+bx+c（a＞0）；
②借助二次函数图象，可以得到相应的一元二次中a，b，c满足的条件，列表如下：
方程根的几何意义：请将（2）补充完整
（1）参考小明的做法，把上述表格补充完整；
（2）若一元二次方程mx2-（2m+3）x-4m=0有一个负实根，一个正实根，且负实根大于-1，求实数m的取值范围．
有这样一个问题：关于x 的一元二次方程a x2+bx+c=0（a＞0）有两个不相等的且非零的实数根．探究a，b，c满足的条件．
小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：
①设一元二次方程ax2+bx+c=0（a＞0）对应的二次函数为y=ax2+bx+c（a＞0）；
②借助二次函数图象，可以得到相应的一元二次中a，b，c满足的条件，列表如下：
方程根的几何意义：请将（2）补充完整
| 方程两根的情况 | 对应的二次函数的大致图象 | a，b，c满足的条件 |
| 方程有两个 不相等的负实根 | 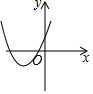 | $\left\{\begin{array}{l}a＞0\\△={b^2}-4ac＞0\\-\frac{b}{2a}＜0\\ c＞0.\end{array}\right.$ |
| 方程有一个负实根，一个正实根 | 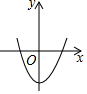 | $\left\{\begin{array}{l}a＞0\\ c＜0.\end{array}\right.$ |
| 方程有两个 不相等的正实根 | 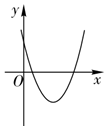 | $\left\{\begin{array}{l}a＞0\\△={b^2}-4ac＞0\\-\frac{b}{2a}＞0\\ c＞0.\end{array}\right.$ |
（2）若一元二次方程mx2-（2m+3）x-4m=0有一个负实根，一个正实根，且负实根大于-1，求实数m的取值范围．
15．
如图所示，数轴上点A、B对应的有理数分别为a、b，下列说法正确的是（ ）
如图所示，数轴上点A、B对应的有理数分别为a、b，下列说法正确的是（ ）| A． | ab＞0 | B． | a+b＞0 | C． | |a|-|b|＜0 | D． | a-b＜0 |