Question

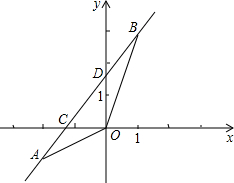如图，已知一次函数y=kx+b的图象经过A（-2，-1），B（1，3）两点，并且交x轴于点C，交y轴于点D．
（1）求一次函数的解析式；
（2）求点C和点D的坐标；
（3）求△AOB的面积．

Answer 1

考点：待定系数法求一次函数解析式

专题：

分析：（1）先把A点和B点坐标代入y=kx+b得到关于k、b的方程组，解方程组得到k、b的值，从而得到一次函数的解析式；
（2）令x=0，y=0，代入y=

4

3

x+

5

3

即可确定C、D点坐标；
（3）根据三角形面积公式和△AOB的面积=S_△AOD+S_△BOD进行计算即可．

解答：解：（1）把A（-2，-1），B（1，3）代入y=kx+b得

-2k+b=-1 k+b=3

，
解得

k= 4 3 b= 5 3

．
所以一次函数解析式为y=

4

3

x+

5

3

；
（2）令y=0，则0=

4

3

x+

5

3

，解得x=-

5

4

，
所以C点的坐标为（-

5

4

，0），
把x=0代入y=

4

3

x+

5

3

得y=

5

3

，
所以D点坐标为（0，

5

3

），
（3）△AOB的面积=S_△AOD+S_△BOD
=

1

2

×

5

3

×2+

1

2

×

5

3

×1
=

5

2

．

点评：本题考查了待定系数法求一次函数解析式：①先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；②将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；③解方程或方程组，求出待定系数的值，进而写出函数解析式．