题目内容
在△ABC中,若∠A-∠B=∠C,则此三角形是 三角形.
考点:三角形内角和定理
专题:
分析:根据三角形的内角和定理得出∠A+∠B+∠C=180°,代入得出2∠A=180°,求出即可.
解答:解:∵∠A-∠B=∠C,
∴∠A=∠B+∠C,
∵∠A+∠B+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
∴△ABC是直角三角形,
故答案为:直角.
∴∠A=∠B+∠C,
∵∠A+∠B+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
∴△ABC是直角三角形,
故答案为:直角.
点评:本题考查了三角形内角和定理的应用,解此题的关键是求出∠A的度数,注意:三角形的内角和等于180°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列运算正确的是( )
| A、x5+x2=x7 |
| B、(x-2)2=x2-4 |
| C、2x5÷x2=2x3 |
| D、(x2)3=x5 |
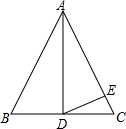 如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是
如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是 如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.
如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.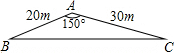 某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要
某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要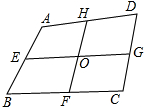 在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点.
在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点. 观察如图所示的长方形.
观察如图所示的长方形.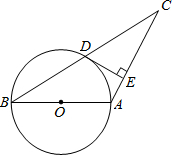 如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.
如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.