题目内容
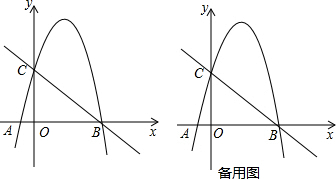
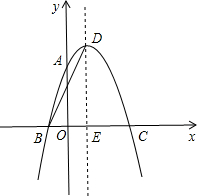 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.
(2)利用顶点坐标公式表示出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.
解答:解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),
∴将A与B坐标代入得:
,
解得:
,
则抛物线解析式为y=-x2+2x+3;
(2)点D为抛物线顶点,由顶点坐标(-
,
)得,D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(-1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD=
=
=2
.
∴将A与B坐标代入得:
|
解得:
|
则抛物线解析式为y=-x2+2x+3;
(2)点D为抛物线顶点,由顶点坐标(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(-1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD=
| BE2+DE2 |
| 22+42 |
| 5 |
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
把直线y=-x-3向上平移2个单位后,得到的直线是( )
| A、y=-x-1 |
| B、y=-x-5 |
| C、y=x-1 |
| D、y=x-5 |
 在平面直角坐标系xOy中,等腰△OAD的底边OA在x轴上,顶点D(2,-4a)(a≠0),抛物线y=a2+bx+c经过O,A,D三点.
在平面直角坐标系xOy中,等腰△OAD的底边OA在x轴上,顶点D(2,-4a)(a≠0),抛物线y=a2+bx+c经过O,A,D三点.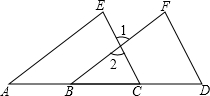 (1)如图,点A、B、C、D在一条直线上,填写下列空格:
(1)如图,点A、B、C、D在一条直线上,填写下列空格: