题目内容
13．在一个不透明的口袋中，有3个红球、2个黄球、1个白球，它们除颜色外不同之外其它完全相同，现从口袋中随机摸出一个球记下颜色后不放回，再随机摸出一个球，则两次都摸到红球的概率是$\frac{1}{5}$．分析 先画树状图展示所有30种等可能的结果数，再找出两次都摸到红球的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有30种等可能的结果数，其中两次都摸到红球的结果数为6，
所以两次都摸到红球的概率=$\frac{6}{30}$=$\frac{1}{5}$．
故答案为$\frac{1}{5}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
相关题目
3．
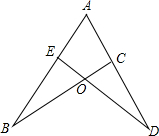如图，若已知AE=AC，用“SAS”说明△ABC≌△ADE，还需要的一个条件是（ ）
如图，若已知AE=AC，用“SAS”说明△ABC≌△ADE，还需要的一个条件是（ ）| A． | BC=DE | B． | AB=AD | C． | BO=DO | D． | EO=CO |
1．下列各数中，绝对值最大的实数是（ ）
| A． | π | B． | -2 | C． | $\frac{4}{3}$ | D． | -$\sqrt{7}$ |
18．
如图，DE∥GF，A在DE上，C在GF上△ABC为等边三角形，其中∠EAC=80°，则∠BCG度数为（ ）
如图，DE∥GF，A在DE上，C在GF上△ABC为等边三角形，其中∠EAC=80°，则∠BCG度数为（ ）| A． | 10° | B． | 20° | C． | 25° | D． | 30° |
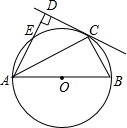如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E．
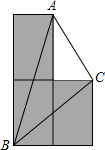用3块形状、大小先完全相同的长方形小木片，拼成知图所示的“L”形，点A，B，C分别是其中的3个顶点，若AB=8cm，CB=6cm，则AC=2$\sqrt{5}$cm．
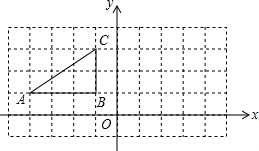如图，方格纸中的每个小方格都是边长为1个单位的正方形．Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（-4，1），点B的坐标为（-1，1）．