题目内容
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
| x | … | ﹣2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
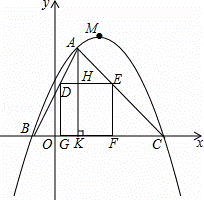
解:(1)由图表可得:抛物线的顶点坐标为:(4,9),
设函数解析式为:y=a(x﹣4)2 +9(a≠0),
+9(a≠0),
把点(0,5)代入y=a(x﹣4)2+9,
解得:a=﹣ .
.
∴函数解析式为:y=﹣ (x﹣4)2+9;
(x﹣4)2+9;
(2)设正方形DEFG的边长为m,
∵AK⊥x轴,
∴∠AKC=90°,
∵∠DEF=∠EFG=90°,
∴四边形HEFK为矩形,
∴HK=EF=m,
∵点A在抛物线y=﹣ (x﹣4)2+9上,横坐标为2,
(x﹣4)2+9上,横坐标为2,
∴y=﹣ (x﹣4)2+9=8,
(x﹣4)2+9=8,
∴点A的坐标为:(2,8),
∴AK=8,∴AH=AK﹣HK=8﹣m,
由题意可得:B(﹣2,0),C(10,0),
∴BC=12,
∵DE∥BC,
∴△ADE∽△ABC,
∴ =
= ,
,
∴ =
= ,
,
∴m=﹣ ,
,
∴正方形的边长为: ;
;
(3)存在,
理由:过顶点M作抛物线的对称轴直线l:x=4,
设点A关于直线l:x=4对称点为A′,A′点的坐标为:(6,8),
∴设AB所在直线解析式为:y=kx+b,
∴ ,
,
解得: ,
,
∴AB所在直线解析式为:y=2x+4,
∵D在直线AB上,DG= ,
,
∴点D的纵坐标为: ,
,
由2x+4= ,
,
解得:x= ,
,
∴点D的坐标为:( ,
, ),
),
设点D关于x轴对称点为D′,则D′( ,﹣
,﹣ ),
),
连接A′D′交对称轴于点P,交x轴于点Q,连接AP,DQ,
则四边形ADQP的周长最小,
设直线A′D′的解析式为:y=k′x+b′,
∴ ,
,
解得: ,
,
∴直线A′D′的解析式为:y= x﹣
x﹣ ,
,
当x=4时,y= ×4﹣
×4﹣ =
= ,∴P(4,
,∴P(4, ),
),
当y=0时,x= ,
,
∴Q点坐标为:( ,0).
,0).


 优学名师名题系列答案
优学名师名题系列答案 x2
x2 ﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件.
﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件. [来源:学科网ZXXK]
[来源:学科网ZXXK] x+2的图象与x轴交于点B,与反比例函数y=
x+2的图象与x轴交于点B,与反比例函数y=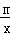 的图象的交点为A(﹣2,3).
的图象的交点为A(﹣2,3).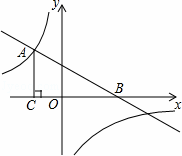

 +
+ =1.
=1.