题目内容
一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为
8 ．
考点： 三角形三边关系．.
分析： 首先设第三边长为x，根据三角形的三边关系可得3﹣2＜x＜3+2，然后再确定x的值，进而可得周长．
解答： 解：设第三边长为x，
∵两边长分别是2和3，
∴3﹣2＜x＜3+2，
即：1＜x＜5，
∵第三边长为奇数，
∴x=3，
∴这个三角形的周长为2+3+3=8，
故答案为：8．
点评： 此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．
练习册系列答案
相关题目
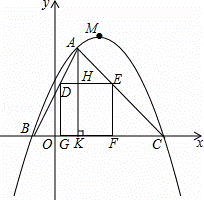
= 如图，在平面直角坐标系xOy中，以M为顶点的抛物线与x轴分别相交于B，C两点，抛物线上一点A的横坐标为2，连接AB，AC，正方形DEFG的一边GF在线段BC上，点D，E在线段AB，AC上，AK⊥x轴于点K，交DE于点H，下表给出了这条抛物线上部分点（x，y）的坐标值：
| x | … | ﹣2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
（1）求出这条抛物线的解析式；
（2）求正方形DEFG的边长；
（3）请问在抛物线的对称轴上是否存在点P，在x轴上是否存在点Q，使得四边形ADQP的周长最小？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
）
，其中a=﹣3．
，运用小聪同学探究的结论，求正方形的边长及MN的长．
B． 
C． 
D． 