Question

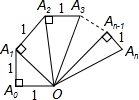图中的螺旋形由一系列直角三角形组成，每个三角形都以点O为一顶点，
（1）求∠A₀OA₁，∠A₁OA₂，∠A₂OA₃的大小；
（2）已知∠A_n-1OA_n是第一个小于20°的角，求n的值．

Answer 1

考点：解直角三角形

专题：

分析：（1）根据A₀A₁，OA₀，A₁O，A₂O，A₁A₂，A₂A₃的值，即可求得∠A₀OA₁，∠A₁OA₂，∠A₂OA₃的大小；
（2）观察图中线段长度求出一系列角的正切值，根据tan∠A_n-1OA_n＜tan20°即可解题．

解答：解：（1）∵tan∠A₀OA₁=1，
∴∠A₀OA₁=45°，
∵tan∠A₁OA₂=

A1A2

OA1

=

2

2

，
∴∠A₁OA₂=arctan

2

2

，
∵tan∠A₂OA₃=

A2A3

OA2

=

3

3

，
∴∠A₂OA₃=30°；
（2）tan∠A_n-1OA_n=

n

n

＜tan20°=0.36，
整理得0.36

n

＞1，
n取最小自然数得n=8，

点评：本题考查了直角三角形中正切值的计算，考查了学生从题干中发现规律的能力，本题中找出规律是解题的关键．