题目内容
生活中处处有数学,表一是某月的日历表,用一个正方形框出3×3=9个数(如图),
(1)在表中框出九个数之和最大的正方形;
(2)若一个正方形内九个数字之和是108,求出它中间的数字;
(3)将自然数1至2014按表二的方式排列,框出九个数其和能为2016吗?若能,求出该方框中的最小数,若不能,请说明理由.

(1)在表中框出九个数之和最大的正方形;
(2)若一个正方形内九个数字之和是108,求出它中间的数字;
(3)将自然数1至2014按表二的方式排列,框出九个数其和能为2016吗?若能,求出该方框中的最小数,若不能,请说明理由.

考点:一元一次方程的应用
专题:
分析:(1)根据表格容易找到九个数之和最大的正方形,中间数字为22;
(2)设中间数字为a,根据九个数之间的联系即可列出方程,解方程即可;
(3)和(2)一样,设中间数字为a,根据九个数之间的联系即可列出方程9a=2016,解方程求出x=224,但是224在第7列,由此即可判定这样的九个数不存在.
(2)设中间数字为a,根据九个数之间的联系即可列出方程,解方程即可;
(3)和(2)一样,设中间数字为a,根据九个数之间的联系即可列出方程9a=2016,解方程求出x=224,但是224在第7列,由此即可判定这样的九个数不存在.
解答:解:(1)如图,红颜色框,是九个数之和最大的正方形;

(2)设中间数字为a,
则9a=108,
解得a=12;
(3)依题意得9a=2016,
∴a=224,
∵224÷7=32,
∴224在第7列,
故这样的九个数不存在.

(2)设中间数字为a,
则9a=108,
解得a=12;
(3)依题意得9a=2016,
∴a=224,
∵224÷7=32,
∴224在第7列,
故这样的九个数不存在.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
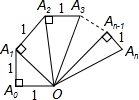 图中的螺旋形由一系列直角三角形组成,每个三角形都以点O为一顶点,
图中的螺旋形由一系列直角三角形组成,每个三角形都以点O为一顶点,