题目内容
2. 已知:如图,△ABC中,AC=BC,CD⊥AB,垂足是D,点E是线段CD上一点,AE的延长线交BC于F.过B作AC的平行线交AE的延长线于G.
已知:如图,△ABC中,AC=BC,CD⊥AB,垂足是D,点E是线段CD上一点,AE的延长线交BC于F.过B作AC的平行线交AE的延长线于G.(1)求证:∠G=∠CBE;
(2)若AE=2EF,那么GF和EF有何数量关系?请写出你的结论并予以证明;
(3)若AE=nEF(其中n>1),那么GF和EF又有何数量关系?请直接写出你的结论,不必证明.
分析 (1)根据等腰三角形的性质得到∠ACD=∠BCD,证明△ACE≌△BCE,得到∠CAE=∠CBE,根据平行线的性质得到∠CAE=∠G,等量代换得到答案;
(2)作FH∥AB交CD于H,根据平行线分线段成比例定理求出GF=FA,根据已知条件计算即可;
(3)与(2)的作法类似,结果用n表示即可.
解答 (1)证明:∵AC=BC,CD⊥AB,
∴∠ACD=∠BCD,AD=BD,
在△ACE和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACE=∠BCE}\\{CE=CE}\end{array}\right.$,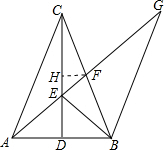
∴△ACE≌△BCE,
∴∠CAE=∠CBE,
∵BG∥AC,
∴∠CAE=∠G,
∴∠G=∠CBE;
(2)如图,作FH∥AB交CD于H,
∴$\frac{FH}{AD}$=$\frac{FE}{EA}$=$\frac{1}{2}$,又AD=BD,
∴HF=$\frac{1}{2}$DB,
∵FH∥AB,
∴$\frac{CF}{CB}$=$\frac{HF}{BD}$=$\frac{1}{2}$,
∴CF=BF,
∵BG∥AC,
∴$\frac{GF}{FA}$=$\frac{BF}{FC}$=1,
∴GF=FA,又AE=2EF,
∴GF=3EF;
(3)∵AE=nEF,
∴$\frac{EF}{EA}$=$\frac{1}{n}$,
由(2)得,$\frac{CF}{CB}$=$\frac{HF}{BD}$=$\frac{1}{n}$,
∴$\frac{CF}{FB}$=$\frac{1}{n-1}$,
∴$\frac{GF}{FA}$=n-1,
∵AE=nEF,
∴FA=(n+1)FE,
∴GF=(n2-1)EF.
点评 本题考查的是相似三角形的判定和性质、全等三角形的判定和性质以及平行线分线段成比例定理的应用,掌握等腰三角形的三线合一、相似三角形的判定定理是解题的关键.

 53随堂测系列答案
53随堂测系列答案| A. | $\frac{5}{7}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{14}$ |
 如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )
如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )| A. | 10° | B. | 20° | C. | 40° | D. | 80° |
 如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )
如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
| A. | y=(x+1)2 | B. | y=(x-1)2 | C. | y=x2+1 | D. | y=x2-1 |
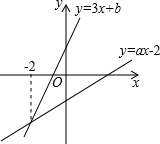 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2. 如图,AB∥CD,直线PQ交AB、CD于点M、N,ME平分∠PMB,NF平分∠PND.求证:ME∥NF.
如图,AB∥CD,直线PQ交AB、CD于点M、N,ME平分∠PMB,NF平分∠PND.求证:ME∥NF.