Question

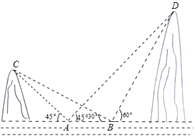
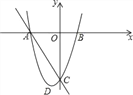
【题目】如图，抛物线的图象与x轴交于A、B两点，点A在点B的左边，与y轴交于点C，点D是抛物线的顶点，且A（﹣6，0），D（﹣2，﹣8）．

（1）求抛物线的解析式；

（2）点P是直线AC下方的抛物线上一动点，不与点A、C重合，求过点P作x轴的垂线交于AC于点E，求线段PE的最大值及P点坐标；

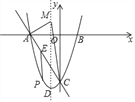
（3）在抛物线的对称轴上足否存在点M，使得△ACM为直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=x2+2x﹣6；（2）最大值为， P点坐标为（﹣3，﹣）；（3）存在,理由见解析.

【解析】分析：设抛物线的解析式为：把点A坐标代入运算即可.

（2）易求得直线AC解析式，即可求得PE长度随横坐标x的变化的二次函数式，求得二次函数的最大值即可解题；
（3）存在3种情况：①∠ACM=90°，②∠CAM=90°，③∠AMC=90°，分类讨论即可求得M的值，即可解题．

详解：（1）设抛物线的解析式为

把代入得 解得

∴抛物线的解析式为，即

（2）如图，当x=0时，，则

设直线AC解析式为y=kx+b，把,代入得，解得

∴直线AC解析式为y=x6，

设则

∴

当时，PE的长度有最大值，最大值为，此时P点坐标为

（3）存在．

抛物线的对称轴为直线

设

∵,

∴

当，为直角三角形，即解得t=4，此时M点坐标为

当，为直角三角形，即解得，此时M点坐标为

当,为直角三角形，即解得 此时M点坐标为 或

综上所述，M点的坐标为或或或