Question

【题目】如图，在矩形中，沿着对角线翻折能与重合，且与交于点，若，则的面积为__________.

Answer 1

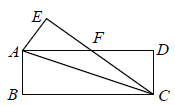
【答案】

【解析】

由矩形的性质及翻折变换先证AF=CF，再在Rt△CDF中利用勾股定理求出CF的长，可通过S△AFC=AFCD求出△ACF的面积．

∵四边形ABCD为矩形，
∴∠D=90°，AD∥BC，CD=AB=1，AD=BC=3，
∴∠FAC=∠ACB，
又∵∠B沿着对角线AC翻折能与∠E重合，
∴∠ACB=∠ACF，
∴∠FAC=∠ACF，
∴FA=FC，
在Rt△DFC中，
设FC=x，则DF=AD-AF=3-x，
∵DF2+CD2=CF2，
∴（3-x）2+12=x2，
解得，x=，
∴AF=，
∴S△AFC=AFCD
=××1
=.

故答案是：．