题目内容
1．
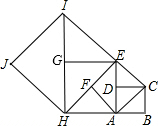如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去…，已知正方形ABCD的面积S1为1，按上述方法所作的正方形的面积依次为S2，S3，…，Sn（n为正整数），那么第Sn个正方形的面积（ ）| A． | 2n | B． | 2n | C． | 2n-1 | D． | 2n+1 |
分析 根据正方形的性质易得：正方形的对角线是正方形的边长的$\sqrt{2}$倍；进而根据题意，找到第二个正方形与第一个正方形面积的关系，依此类推，可得第n个正方形Sn的面积．
解答 解：根据勾股定理得：正方形的对角线是正方形的边长的$\sqrt{2}$倍；
即第二个正方形的面积是第一个正方形面积的2倍，即是2，…
依此类推第n个正方形的面积是上一个正方形面积的2倍，即2×2×2×…×2（n-1个2）=2n-1．
故选C．
点评 本题要求学生能够根据勾股定理得到前后正方形的边长之间的关系，进一步得到面积之间的关系．从而找到规律．
练习册系列答案
阅读快车系列答案
相关题目
12．下列说法中正确的个数是（ ）
①两个三角形中，有两条边对应相等，则可以用“HL”来判定这两个三角形全等；
②有一条直角边和一个锐角对应相等的两个三角形全等；
③有两条直角边分别相等的两个直角三角形全等；
④两锐角对应相等的两个直角三角形全等．
①两个三角形中，有两条边对应相等，则可以用“HL”来判定这两个三角形全等；
②有一条直角边和一个锐角对应相等的两个三角形全等；
③有两条直角边分别相等的两个直角三角形全等；
④两锐角对应相等的两个直角三角形全等．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．尺规作图是指（ ）
| A． | 用直尺和圆规作图 | B． | 用直尺规范作图 | ||
| C． | 用刻度尺和圆规作图 | D． | 用没有刻度的直尺和圆规作图 |
16．某班45名同学在一次数学测验中，25名男生的平均得分为m，20名女生的平均得分为n，这个班的所有同学的平均得分是（ ）
| A． | $\frac{m+n}{25}$ | B． | $\frac{25m+20n}{45}$ | C． | $\frac{m+n}{2}$ | D． | $\frac{20（m+n）}{45}$ |