题目内容
6.观察下面的一列数,按这种规律在横线上填上恰当的数:$\frac{1}{3}$,-$\frac{2}{15}$,$\frac{3}{35}$,-$\frac{4}{63}$,$\frac{5}{99}$,-$\frac{6}{143}$…
分析 由前4个数得出第n个数为(-1)n+1•$\frac{n}{(2n)^{2}-1}$,据此可得.
解答 解:∵第1个数$\frac{1}{3}$=(-1)2×$\frac{1}{{2}^{2}-1}$,
第2个数-$\frac{2}{15}$=(-1)3×$\frac{2}{{4}^{2}-1}$,
第3个数$\frac{3}{35}$=(-1)4×$\frac{3}{{6}^{2}-1}$,
第4个数-$\frac{4}{63}$=(-1)5×$\frac{4}{{8}^{2}-1}$,
…
∴第5个数为(-1)6×$\frac{5}{1{0}^{2}-1}$=$\frac{5}{99}$,
第6个数为(-1)7×$\frac{6}{1{2}^{2}-1}$=-$\frac{6}{143}$,
故答案为:$\frac{5}{99}$、-$\frac{6}{143}$.
点评 本题主要考查数字的变化规律,根据已知数列得出第n个数为(-1)n+1•$\frac{n}{(2n)^{2}-1}$是解题的关键.

练习册系列答案
相关题目
16.下列各组单项式中,属于同类项的是( )
| A. | mn与-mn | B. | 4ab与4abc | C. | 2x2y与xy2 | D. | 62与x2 |
17.下列说法中,错误的是( )
| A. | 单项式乘以单项式,其结果一定仍是单项式 | |
| B. | 两个单项式相乘,积的系数是这两个单项式系数的积 | |
| C. | 两个单项式相乘,积的次数是这两个单项式次数的积 | |
| D. | 两个单项式相乘,每一个因式所含字母都在结果里出现 |
1.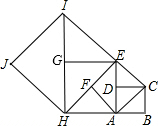 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )
 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )| A. | 2n | B. | 2n | C. | 2n-1 | D. | 2n+1 |
11.下列运动不属于旋转的是( )
| A. | 电风扇的扇叶在不停地转动 | B. | 时针在钟面上不停地转动 | ||
| C. | 单摆上的小球的转动 | D. | 火车在笔直的轨道上飞驰 |
18.下列各组数中,互为相反数的是( )
| A. | -2与-$\frac{1}{2}$ | B. | |-2|与$\frac{1}{2}$ | C. | |-2|与-2 | D. | -|-2|与-2 |
16.下列关系式中,不含有x=-1这个解的是( )
| A. | 2x+1=-1 | B. | 2x+1>-1 | C. | -2x+1≥3 | D. | -2x-1≤3 |
 有理数a、b在数轴上的位置如图所示,则a<-b.(用“>”或“<”号连接)
有理数a、b在数轴上的位置如图所示,则a<-b.(用“>”或“<”号连接)