题目内容
16.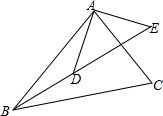 如图所示,E是△ABC外一点,D在BE上,且∠BAD=20°,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求∠EBC的度数.
如图所示,E是△ABC外一点,D在BE上,且∠BAD=20°,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求∠EBC的度数.
分析 根据相似三角形的判定和性质得到∠BAC=∠DAE,∠C=∠E,于是得到∠EAC=∠BAD=20°,由三角形的内角和即可得到结果.
解答 解:∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即:∠EAC=∠BAD=20°,
∴∠EBC=∠EAC=20°.
点评 本题考查了相似三角形的判定和性质,三角形的内角和,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
11.在Rt△ABC中,∠C=90°,如果三角形各边的长度都扩大2倍,则sinA的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 不能确定 |
8.一个不透明的袋中装有除颜色外,其余均相同的5个红球和2个黄球,从中随机摸出一个,摸到红球的概率是 ( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{2}{5}$ |
5.某商品连续两次降价,售价由原来的1185元降到了580元.设平均每次降价的百分率为x,则根据题意列出的方程是( )
| A. | 580(1+x%)2=1185 | B. | 1185(1+x)2=580 | C. | 1185(1-x%)2=580 | D. | 1185(1-x)2=580 |

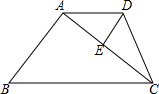 已知:梯形ABCD中,AD∥BC,AD=2,DC=3,AB=4,BC=5,DE平分∠ADC,求线段DE的长.
已知:梯形ABCD中,AD∥BC,AD=2,DC=3,AB=4,BC=5,DE平分∠ADC,求线段DE的长.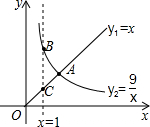 函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则下列结论:
函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则下列结论: