题目内容
2.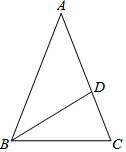 如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,$BC=\sqrt{5}$,BD=2.
如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,$BC=\sqrt{5}$,BD=2.(1)求证:△BCD是直角三角形.
(2)求△ABC的面积.
分析 (1)根据勾股定理的逆定理直接得出结论;
(2)设腰长为x,在直角三角形ADB中,利用勾股定理列出x的方程,求出x的值,进而利用三角形的面积公式求出答案.
解答 解:(1)∵CD=1,$BC=\sqrt{5}$,BD=2,
∴CD2+BD2=BC2,
∴△BDC是直角三角形;
(2)设腰长AB=AC=x,
在Rt△ADB中,
∵AB2=AD2+BD2,
∴x2=(x-1)2+22,
解得x=$\frac{5}{2}$,
即△ABC的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×$\frac{5}{2}$×2=$\frac{5}{2}$.
点评 本题主要考查了勾股定理的逆定理以及等腰三角形的性质,解题的关键是利用勾股定理求出腰长,此题难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
 已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )| A. | y<-4 | B. | y<-2 | C. | -2<y<0 | D. | -4<y<0 |
14.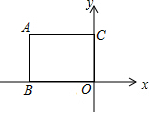 如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
 如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )| A. | (-5,3) | B. | (5,-3) | C. | (-3,5) | D. | (3,-5) |
11.在平面直角坐标系内有一点A的坐标是(-3,5),则点A到y轴的距离是( )
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |
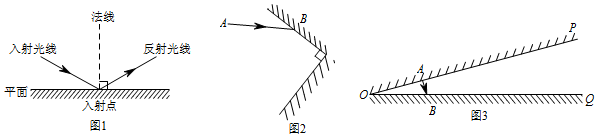
 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.
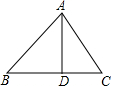 如图,在△ABC中,AD⊥BC交BC于点D,若BC=14,AD=12,tan∠BAD=$\frac{3}{4}$,则DC的长为( )
如图,在△ABC中,AD⊥BC交BC于点D,若BC=14,AD=12,tan∠BAD=$\frac{3}{4}$,则DC的长为( )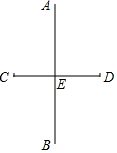 如图,直线AB是线段CD的垂直平分线,则下列结论正确的有( )
如图,直线AB是线段CD的垂直平分线,则下列结论正确的有( )