题目内容
已知a,b是正整数.
(1)若
是整数,则满足条件的a的值为 ;
(2)若
+
是整数,则满足条件的有序数对(a,b)为 .
(1)若
|
(2)若
|
|
考点:估算无理数的大小
专题:
分析:(1)7=7×1,根据以上算式的长即可;
(2)根据二次根式的性质和已知得出即可.
(2)根据二次根式的性质和已知得出即可.
解答:解:(1)∵
是整数,a是正整数,
∴a=7,
故答案为:7;
(2)∵
+
是整数,
∴a=7,b=10或a=28,b=40,
因为当a=7,b=10时,
+
=1+1=2是整数;
当a=28,b=40时,
+
=
+
=1是整数;
即满足条件的有序数对(a,b)为(7,10)或(28,40),
故答案为:(7,10)或(28,40).
|
∴a=7,
故答案为:7;
(2)∵
|
|
∴a=7,b=10或a=28,b=40,
因为当a=7,b=10时,
|
|
当a=28,b=40时,
|
|
| 1 |
| 2 |
| 1 |
| 2 |
即满足条件的有序数对(a,b)为(7,10)或(28,40),
故答案为:(7,10)或(28,40).
点评:本题考查了二次根式的性质和二次根式的运算,估算无理数的大小的应用,题目比较好,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是( )
| A、a6÷a2=a3 |
| B、a3•a3•a3=3a3 |
| C、(a3)4=a12 |
| D、(a+2b)2=a2+4b2 |
下列计算,正确的是( )
| A、a6÷a2=a3 |
| B、3a2×2a2=6a2 |
| C、(ab2)2=a2b4 |
| D、5a+3a=8a2 |
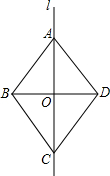 如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:
如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论: