题目内容
3.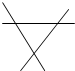 如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )
如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )| A. | 4处 | B. | 3处 | C. | 2处 | D. | 1处 |
分析 由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
解答 解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选:A.
点评 本题考查了角平分线的性质.掌握角平分线上的点到角两边的距离相等是解题的关键,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法错误的是( )
| A. | 任何一个有理数的绝对值都是正数 | |
| B. | 有理数可以分为正有理数,负有理数和零 | |
| C. | 两个有理数和为正数,这两个数不可能都为负数 | |
| D. | 0既不是正数也不是负数 |
15. 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )| A. | 180°-α | B. | 90°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
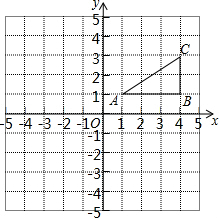 如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).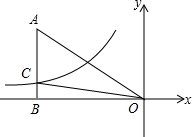 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )