��Ŀ����
14����֪��ͼ1����ADEB�У�AD��MN��BE��MN������ֱ�Ϊ��D����E����C��MN�ϣ�CD=BE����ACB=90�㣮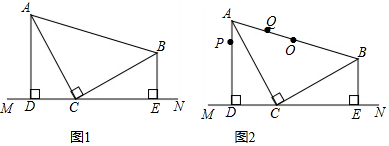
��1����֤����ACD=��CBE��
��2����DE=8��������ADEB�������
��3����ͼ2��������ADEB���ܳ�Ϊm��AB���е�O������������P��Qͬʱ����������O��A��D��E��B��O�ķ����ƶ�����P���ٶ��ǵ�Q��3��������Q��һ�ε���B��ʱ������ͬʱֹͣ�ƶ���
������ͬʱֹͣʱ����P�ƶ���·�����Q�ƶ���·��֮�2m�����������������=����
���ƶ������У���P�ܷ�͵�Q����������ܣ�����ֱ��l����������͵�O����̽��ֱ��l��AB��λ�ù�ϵ��д���������̣�������ܣ�д�����ɣ�
���� ��1������ͬ�ǵ������ȣ�����֤����
��2��ֻҪ֤����ADC�ա�CEB���ɵ�AD=CE���Ƴ�AD+BE=CD+CE=DE=8������S����ADEB=$\frac{1}{2}$•��AD+BE��•DE���㼴�ɣ�
��3��������ֹͣʱ��Q���˶�·��=OA+AD+DE+BE��P�˶���·��=3��OA+AD+DE+BE����·�̲�=2��OA+AD+DE+BE�����ɴ˼����жϣ�
�ڽ��ۣ�ֱ��l��AB��ֻҪ֤������ʱ�������ڵ�C�����ɽ�����⣻
��� ��1��֤������ͼ1�У�
��AD��MN��BE��MN��
���ADC=��CEB=��ACB=90�㣬
���ACD+��BCE=90�㣬��BCE+��CBE=90�㣬
���ACD=��CBE��
��2���⣺�ڡ�ADC�͡�CEB�У�
$\left\{\begin{array}{l}{��ACD=��CBE}\\{CD=BE}\\{��ADC=��CEB}\end{array}\right.$��
���ADC�ա�CEB��
��AD=CE��
��AD+BE=CD+CE=DE=8��
��S����ADEB=$\frac{1}{2}$•��AD+BE��•DE=32��
��3���ٽ⣺��ͼ2�У�
����ֹͣʱ��Q���˶�·��=OA+AD+DE+BE��P�˶���·��=3��OA+AD+DE+BE����
·�̲�=2��OA+AD+DE+BE����
��OA+AD+DE+BE��m��
��·�̲2m��
�ʴ�Ϊ����
�ڽ��ۣ�ֱ��l��AB���������£�
���Q���˶��ٶ�ΪV�����P���˶��ٶ�Ϊ3V���˶�ʱ��Ϊt��
����ʱ��3Vt-Yt=m��
��Vt=$\frac{m}{2}$��
�ɣ�1����֪AD=CE��CD=BE��OA=OB��
������ʱ��Q����P�ڵ�C����
�ߡ�ADC�ա�CEB��
��AC=CB����OA=OB��
��OC��AB����ֱ��l��AB��
���� ���⿼���ı����ۺ��⡢ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ����ε������ʽ��·�̡��ٶȡ�ʱ��Ĺ�ϵ��֪ʶ������Ĺؼ����������⣬���������ѧ֪ʶ������⣬�����п�ѹ���⣮

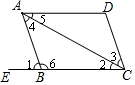 ��ͼ���ı���ABCD��E��CB�ӳ�����һ�㣬����������ȷ���ǣ�������
��ͼ���ı���ABCD��E��CB�ӳ�����һ�㣬����������ȷ���ǣ�������| A�� | �����1=��2����ôAB��CD | B�� | �����3=��4����ôAD��BC | ||
| C�� | ���AD��BC����ô��6+��BAD=180�� | D�� | �����6+��BCD=180�㣬��ôAD��BC |
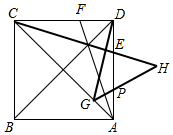 ��������ABCD�У�DE=DF��DG��CE����CA��G��GH��AF����AD��P����CE�ӳ�����H��������������DG��GH��CH��������ϵ��
��������ABCD�У�DE=DF��DG��CE����CA��G��GH��AF����AD��P����CE�ӳ�����H��������������DG��GH��CH��������ϵ��