题目内容
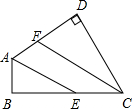如图，已知在四边形ABCD中，∠B=∠D=90°，AE、CF分别是∠DAB及∠DCB的平分线．求证：AE∥CF．考点：平行线的判定
专题：证明题
分析：由四边形的内角和推出∠DAB与∠DCB互补，由角平分线推出∠DAE与∠DCF互余，再由∠DFC与∠DCF互余推出∠DFC=∠DAE，即可证得．
解答：证明：∵∠B=∠D=90°，∠BAD+∠B+∠BCD+∠D=360°，
∴∠DAB+∠DCB=180°，
∵AE、CF分别是∠DAB及∠DCB的平分线、
∴∠DAE+∠DCF=90°，
又∠DFC+∠DCF=90°，
∴∠DFC=∠DAE，
∴AE∥CF．
∴∠DAB+∠DCB=180°，
∵AE、CF分别是∠DAB及∠DCB的平分线、
∴∠DAE+∠DCF=90°，
又∠DFC+∠DCF=90°，
∴∠DFC=∠DAE，
∴AE∥CF．
点评：本题考查四边形的内角和、角平分线的定义、互余和互补的性质、及平行线的判定，较难．
练习册系列答案
相关题目
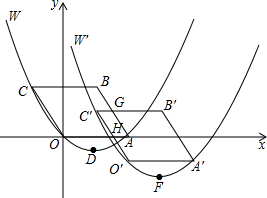综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（-2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．
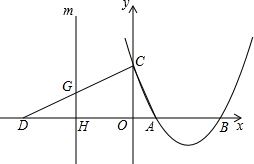如图，抛物线y=ax2-8ax+12a（a＞0）与x轴交于A、B两点（A在B的左侧），与y轴交于点C，点D的坐标为（-6，0），且∠ACD=90°．