题目内容
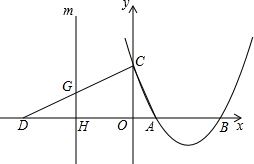 如图,抛物线y=ax2-8ax+12a(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(-6,0),且∠ACD=90°.
如图,抛物线y=ax2-8ax+12a(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(-6,0),且∠ACD=90°.(1)请直接写出A、B两点的坐标;
(2)求抛物线的解析式;
(3)抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标及周长的最小值;若不存在,说明理由;
(4)平行于y轴的直线m从点D出发沿x轴向右平行移动,到点A停止.设直线m与折线DCA的交点为G,与x轴的交点为H(t,0).记△ACD在直线m左侧部分的面积为s,求s关于t的函数关系式及自变量t的取值范围.
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)令y=ax2-8ax+12a=0,解一元二次方程,求出点A、B的坐标;
(2)由∠ACD=90°可知△ACD为直角三角形,利用勾股定理,列出方程求出a的值,进而求出抛物线的解析式;
(3)△PAC的周长=AC+PA+PC,AC为定值,则当PA+PC取得最小值时,△PAC的周长最小.设点C关于对称轴的对称点为C′,连接AC′与对称轴交于点P,由轴对称的性质可知点P即为所求;
(4)直线m运动过程中,有两种情形,需要分类讨论并计算,避免漏解.
(2)由∠ACD=90°可知△ACD为直角三角形,利用勾股定理,列出方程求出a的值,进而求出抛物线的解析式;
(3)△PAC的周长=AC+PA+PC,AC为定值,则当PA+PC取得最小值时,△PAC的周长最小.设点C关于对称轴的对称点为C′,连接AC′与对称轴交于点P,由轴对称的性质可知点P即为所求;
(4)直线m运动过程中,有两种情形,需要分类讨论并计算,避免漏解.
解答:解:(1)抛物线的解析式为:y=ax2-8ax+12a(a>0),
令y=0,即ax2-8ax+12a=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)抛物线的解析式为:y=ax2-8ax+12a(a>0),
令x=0,得y=12a,∴C(0,12a),OC=12a.
在Rt△COD中,由勾股定理得:CD2=OC2+OD2=(12a)2+62=144a2+36;
在Rt△AOC中,由勾股定理得:AC2=OC2+OA2=(12a)2+22=144a2+4;
在Rt△ACD中,由勾股定理得:DC2+AC2=AD2;
即:(144a2+36)+(144a2+4)=82,
解得:a=
或a=-
(舍去),
∴抛物线的解析式为:y=
x2-
x+2
.
(3)存在.
对称轴为直线:x=-
=4.

由(2)知C(0,2
),则点C关于对称轴x=4的对称点为C′(8,2
),
连接AC′,与对称轴交于点P,则点P为所求.此时△PAC周长最小,最小值为AC+AC′.
设直线AC′的解析式为y=kx+b,则有:
,解得
,
∴y=
x-
.
当x=4时,y=
,∴P(4,
).
过点C′作C′E⊥x轴于点E,则C′E=2
,AE=6,
在Rt△AC′E中,由勾股定理得:AC′=
=4
;
在Rt△AOC中,由勾股定理得:AC=
=4.
∴AC+AC′=4+4
.
∴存在满足条件的点P,点P坐标为(4,
),△PAC周长的最小值为4+4
.
(4)①当-6≤t≤0时,如答图4-1所示.
∵直线m平行于y轴,
∴
=
,即
=
,解得:GH=
(6+t)
∴S=S△DGH=
DH•GH=
(6+t)•
(6+t)=
t2+2
t+6
;

②当0<t≤2时,如答图4-2所示.
∵直线m平行于y轴,
∴
=
,即
=
,解得:GH=-
t+2
.
∴S=S△COD+S梯形OCGH=
OD•OC+
(GH+OC)•OH
=
×6×2
+
(-
t+2
+2
)•t
=-
t2+2
t+6
.
∴S=
.
令y=0,即ax2-8ax+12a=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)抛物线的解析式为:y=ax2-8ax+12a(a>0),
令x=0,得y=12a,∴C(0,12a),OC=12a.
在Rt△COD中,由勾股定理得:CD2=OC2+OD2=(12a)2+62=144a2+36;
在Rt△AOC中,由勾股定理得:AC2=OC2+OA2=(12a)2+22=144a2+4;
在Rt△ACD中,由勾股定理得:DC2+AC2=AD2;
即:(144a2+36)+(144a2+4)=82,
解得:a=
| ||
| 6 |
| ||
| 6 |
∴抛物线的解析式为:y=
| ||
| 6 |
4
| ||
| 3 |
| 3 |
(3)存在.
对称轴为直线:x=-
| 8a |
| 2a |

由(2)知C(0,2
| 3 |
| 3 |
连接AC′,与对称轴交于点P,则点P为所求.此时△PAC周长最小,最小值为AC+AC′.
设直线AC′的解析式为y=kx+b,则有:
|
|
∴y=
| ||
| 3 |
2
| ||
| 3 |
当x=4时,y=
2
| ||
| 3 |
2
| ||
| 3 |
过点C′作C′E⊥x轴于点E,则C′E=2
| 3 |
在Rt△AC′E中,由勾股定理得:AC′=
(2
|
| 3 |
在Rt△AOC中,由勾股定理得:AC=
22+(2
|
∴AC+AC′=4+4
| 3 |
∴存在满足条件的点P,点P坐标为(4,
2
| ||
| 3 |
| 3 |
(4)①当-6≤t≤0时,如答图4-1所示.
∵直线m平行于y轴,
∴
| GH |
| CO |
| DH |
| DO |
| GH | ||
2
|
| 6+t |
| 6 |
| ||
| 3 |
∴S=S△DGH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
| 3 |
| 3 |

②当0<t≤2时,如答图4-2所示.
∵直线m平行于y轴,
∴
| GH |
| CO |
| AH |
| AO |
| GH | ||
2
|
| 2-t |
| 2 |
| 3 |
| 3 |
∴S=S△COD+S梯形OCGH=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
=-
| ||
| 2 |
| 3 |
| 3 |
∴S=
|
点评:本题是典型的二次函数压轴题,综合考查二次函数与一次函数的图象与性质、待定系数法、解一元二次方程、相似、勾股定理等知识点,难度不大.第(3)考查最值问题,注意利用轴对称的性质;第(4)问是动线型问题,考查分类讨论的数学思想,注意图形面积的计算.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列四个数中,负数是( )
| A、|-4| | ||
| B、-(-4)2 | ||
| C、4-4 | ||
D、
|
 为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表:
为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表: 如图:矩形ABCD中,E是AD的中点,将△ABE折叠后,得到△GBE,延长BG交CD于点F,若CF=1,FD=2,求BC的长.
如图:矩形ABCD中,E是AD的中点,将△ABE折叠后,得到△GBE,延长BG交CD于点F,若CF=1,FD=2,求BC的长.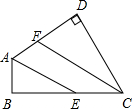 如图,已知在四边形ABCD中,∠B=∠D=90°,AE、CF分别是∠DAB及∠DCB的平分线.求证:AE∥CF.
如图,已知在四边形ABCD中,∠B=∠D=90°,AE、CF分别是∠DAB及∠DCB的平分线.求证:AE∥CF.