题目内容
已知△ABC的三边长分别为a、b、c,且有|
-2|+b+c2+36=4
+12c,试判断△ABC的形状.
| a-6 |
| b-4 |
考点:因式分解的应用
专题:
分析:根据非负数的性质解得各边的长,再根据勾股定理的逆定理判定是否直角三角形.
解答:解:由|
-2|+b+c2+36=4
+12c,得
|
-2|+(c-6)2+(2-
)2=0,
则
-2=0,c-6=0,2-
=0,
解得a=10,c=6,b=8,
故b2+c2=a2,
∵△ABC的三边长分别为a、b、c,
∴△ABC是直角三角形.
| a-6 |
| b-4 |
|
| a-6 |
| b-4 |
则
| a-6 |
| b-4 |
解得a=10,c=6,b=8,
故b2+c2=a2,
∵△ABC的三边长分别为a、b、c,
∴△ABC是直角三角形.
点评:本题考查了因式分解的应用、勾股定理的逆定理、非负数的性质,解题的关键是注意配方法的步骤,在变形的过程中不要改变式子的值.

练习册系列答案
相关题目
 为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表:
为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表:
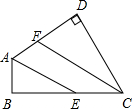 如图,已知在四边形ABCD中,∠B=∠D=90°,AE、CF分别是∠DAB及∠DCB的平分线.求证:AE∥CF.
如图,已知在四边形ABCD中,∠B=∠D=90°,AE、CF分别是∠DAB及∠DCB的平分线.求证:AE∥CF. 如图,AB∥CD,BE⊥DE.则∠B与∠D之间的关系
如图,AB∥CD,BE⊥DE.则∠B与∠D之间的关系 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-