题目内容
某商品连续两次9折降价销售,降价后每件商品的售价为a元,该产品原价为( )
| A、0.92a元 | ||
| B、1.12a元 | ||
C、
| ||
D、
|
考点:列代数式
专题:
分析:可以先设商品的原价为x元,根据等量关系:售价=原价×打折数,可以列出方程,求解即可得到结论.
解答:解:设商品的原价为x元,
则可知第一次打折后价钱为:(x×0.9)元,
当第二次打折时,原价变为(x×0.9×0.9)元,
即打折后售价=(x×0.9)×0.9=a,
解得:x=
.
即可得该商品的原价为
元.
故选:D.
则可知第一次打折后价钱为:(x×0.9)元,
当第二次打折时,原价变为(x×0.9×0.9)元,
即打折后售价=(x×0.9)×0.9=a,
解得:x=
| a |
| 0.81 |
即可得该商品的原价为
| a |
| 0.81 |
故选:D.
点评:此题考查列代数式,解题关键是找到等量关系,列方程辅助解答.

练习册系列答案
相关题目
在平面直角坐标系中,设点P到原点O的距离为p,OP与x轴正方向的夹角为a,则用[p,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为[
,45°].若点Q的极坐标为[2,60°],则点Q的坐标为( )
| 2 |
A、(1,
| ||
B、(1,-
| ||
C、(
| ||
| D、(1,1) |
 如图,为庆祝六一国际儿童节,八年级同学要在广场上布置一个矩形的花坛,计划用“串红”一盆接一盆摆成两条对角线,如果一条对角线用了39盆“串红”,还需要从花房运来“串红”( )
如图,为庆祝六一国际儿童节,八年级同学要在广场上布置一个矩形的花坛,计划用“串红”一盆接一盆摆成两条对角线,如果一条对角线用了39盆“串红”,还需要从花房运来“串红”( )| A、37盆 | B、38盆 |
| C、39盆 | D、40盆 |
已知:1-(3m-5)2有最大值,则方程5m-4=3x+2的解是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
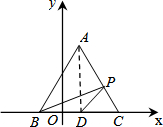 如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2 如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.
如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.