题目内容

5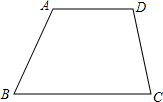．如图，草原上有4口油井，位于四边形ABCD的4个顶点上，现要建一个维修站H，试问维修站H建在何处，才能使它到4口井的距离之和HA+HB+HC+HD为最小？试说明理由．

分析 由两点之间线段最短可知点H位于AC和BD的交点处时，HA+HB+HC+HD最小．

解答 解：如图所示：

理由：∵两点之间线段最短，
∴当点A、H、C在一条直线上，且点B、H、D也在一条直线上时，HA+HB+HC+HD有最小值．

点评 本题主要考查的是作图-应用与设计作图，掌握线段的性质是解题的关键．

练习册系列答案
相关题目
4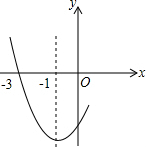．如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3，0）．下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0，④a+b+c=0．其中说法正确的是（　　）
A．①②B．①②③C．①②④D．②③④
5．不等式组$\left\{{\begin{array}{l}{x-3≤0}\\{x+1＞0}\end{array}}\right.$的解集是（　　）
A．-1＜x≤3B．-1＜x＜3C．x＞-1D．x≤3
2．cos60°的算术平方根等于（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{3}$C．$\frac{{\sqrt{2}}}{2}$D．$\sqrt{3}$
9．如图1，点A是线段BC上一点，△ABD和△ACE都是等边三角形．
（1）连接BE，CD，求证：BE=CD；
（2）如图2，作DP∥BC交EA于D′，交EC于P．当线段AB、AC满足什么数量关系时，△BDD′≌△CPD′？并给与证明．
10．解方程：x（3x-2）=6x-4．
17．如图，平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段 OA，OC的长是一元二次方程x2-17x+60=0的两根（OA＞OC），BE=5，tan∠ABO=$\frac{3}{4}$，反比例函数$y=\frac{k}{x}$的图象经过点E

（1）求k的值；
（2）若直线 AB与反比例函数$y=\frac{k}{x}$的图象上除点E外的另一交点为P，求四边形ODEP的面积；
（3）在直线CD下方的反比例函数$y=\frac{k}{x}$图象上是否存在一点Q，使以点C、E、Q为顶点的三角形的面积等于42？若存在，求出符合条件的点 Q的坐标；若不存在，请说明理由．
14．已知一个三角形的底边长是（x2-2x+4）cm，高是4cm，则这个三角形的面积为2x2-4x+8cm2．
15．在下列函数中，当x＞0时，y随x的增大而增大的是（　　）
A．y=-x+1B．y=x2-1C．y=-5xD．y=-x2+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网