题目内容
9.如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.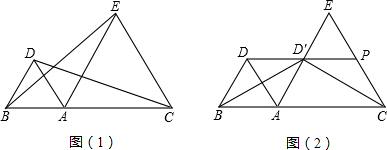
(1)连接BE,CD,求证:BE=CD;
(2)如图2,作DP∥BC交EA于D′,交EC于P.当线段AB、AC满足什么数量关系时,△BDD′≌△CPD′?并给与证明.
分析 (1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,然后求出∠BAE=∠DAC,再利用“边角边”证明△BAE和△DAC全等,根据全等三角形对应边相等即可得证;
(2)当AC=2AB时,△BDD′与△CPD′全等,根据等边三角形的性质和平行线的性质得到四边形ABDD′是菱形,根据菱形的对角线平分一组对角可得∠ABD′=∠DBD′=30°,根据等边三角形的性质求出AC=AE,∠ACE=60°,然后根据等腰三角形三线合一的性质求出∠PCD′=∠ACD′=30°,从而得到∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PD′C=30°,然后利用“角边角”证明△BDD′与△CPD′全等.
解答 (1)证明:∵△ABD和△ACE都是等边三角形.
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
在△BAE和△DAC中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△BAE≌△DAC(SAS),
∴BE=CD;
(2)解:当AC=2AB时,△BDD′与△CPD′全等.
∵∠BAD=∠CAE=60°,
∴∠DAE=180°-60°×2=60°,
∵DP∥BC,
∴∠D′DA=∠DAB=60°,
∴△ADD′是等边三角形,
∴AB=BD=DD′=AD′,
∴四边形ABDD′是菱形,
∴∠ABD′=∠DBD′=$\frac{1}{2}$∠ABD=$\frac{1}{2}$×60°=30°,
∵△ACE是等边三角形,
∴AC=AE,∠ACE=60°,
∵AC=2AB,
∴AE=2AD′,
∴∠PCD′=∠ACD′=$\frac{1}{2}$∠ACE=$\frac{1}{2}$×60°=30°,
又∵DP∥BC,
∴∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PCD′=∠PD′C=30°,
在△BDD′与△CPD′中,
$\left\{\begin{array}{l}{∠DBD′=∠PCD′}\\{BD′=CD′}\\{∠BD′D=∠PD′C}\end{array}\right.$,
∴△BDD′≌△CPD′(ASA).
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,菱形的性质和判定,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.

| A. | +(+3)和+(-3) | B. | +(-5)和-5 | C. | -(+4)和-(-4) | D. | +(-1)和|-1| |
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
| A. | 12×104 | B. | 1.2×105 | C. | 0.12×106 | D. | 1.2×104 |
 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.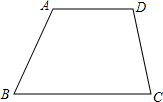 如图,草原上有4口油井,位于四边形ABCD的4个顶点上,现要建一个维修站H,试问维修站H建在何处,才能使它到4口井的距离之和HA+HB+HC+HD为最小?试说明理由.
如图,草原上有4口油井,位于四边形ABCD的4个顶点上,现要建一个维修站H,试问维修站H建在何处,才能使它到4口井的距离之和HA+HB+HC+HD为最小?试说明理由. 一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗?
一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗? 实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.