题目内容
 如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠BEC=
(2)若BC=20cm,则△BCE的周长是
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)先根据等腰三角形的性质得出∠ABC的度数,再由三角形内角和定理求出∠A的度数,根据线段垂直平分线的性质求出AE=BE,故可得出∠ABE的度数,进而可得出结论;
(2)根据AE=BD可知,BE+CE=AE+CE=AC,由此可得出结论.
(2)根据AE=BD可知,BE+CE=AE+CE=AC,由此可得出结论.
解答:解:(1)∵在△ABC中,AB=AC=30cm,∠C=70°,
∴∠ABC=∠C=70°,
∴∠A=180°-∠ABC-∠C=180°-70°-70°=40°.
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=40°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°,
∴∠BEC=180°-∠C-∠EBC=180°-70°-30°=80°.
故答案为:80°;
(2)∵由(1)知AE=BE,
∴BE+CE=AE+CE=AC=30cm,
∵BC=20cm,
∴△BCE的周长=AC+BC=30+20=50(cm).
故答案为:50.

∴∠ABC=∠C=70°,
∴∠A=180°-∠ABC-∠C=180°-70°-70°=40°.
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=40°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°,
∴∠BEC=180°-∠C-∠EBC=180°-70°-30°=80°.
故答案为:80°;
(2)∵由(1)知AE=BE,
∴BE+CE=AE+CE=AC=30cm,
∵BC=20cm,
∴△BCE的周长=AC+BC=30+20=50(cm).
故答案为:50.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若(x+m)(x+n)=x2-6x+5,则( )
| A、m,n同时为负 |
| B、m,n同时为正 |
| C、m,n异号 |
| D、m,n异号且绝对值小的为正 |
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |

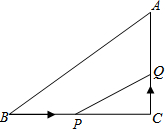 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?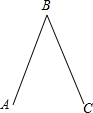 如图,用直尺和圆规画出∠ABC的平分线BM,
如图,用直尺和圆规画出∠ABC的平分线BM,