题目内容
已知抛物线Y=
x2-(m+1)x+m2与x轴有两个交点,回答下列问题:
(1)求m的取值范围;
(2)若两个交点的横坐标的平方和等于16,求m的值.
| 1 |
| 4 |
(1)求m的取值范围;
(2)若两个交点的横坐标的平方和等于16,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)抛物线与x轴有两个交点,可令函数值y=0,则所得方程的△>0,由此可求出m的取值范围;
(2)设两个交点的坐标为m和n,利用根与系数的关系以及已知条件即可求出m的值.
(2)设两个交点的坐标为m和n,利用根与系数的关系以及已知条件即可求出m的值.
解答:解:(1)∵抛物线与x轴有两个交点,
∴△=b2-4ac>0
即:(m+1)2-4×
×m2>0,
解得,m>-
;
(2)设两个交点的坐标为c和d,
∴c+d=-
=4(m+1),cd=4m2,
∵两个交点的横坐标的平方和等于16,
∴c2+d2=16,
∴16(m+1)2-8m2=16,
解得:m=0或-4.
∴△=b2-4ac>0
即:(m+1)2-4×
| 1 |
| 4 |
解得,m>-
| 1 |
| 2 |
(2)设两个交点的坐标为c和d,
∴c+d=-
| b |
| a |
∵两个交点的横坐标的平方和等于16,
∴c2+d2=16,
∴16(m+1)2-8m2=16,
解得:m=0或-4.
点评:此题考查了二次函数与一元二次方程的关系、根的判别式、二次函数解析式的确定等知识的综合应用.

练习册系列答案
相关题目
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
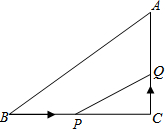 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?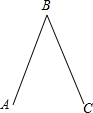 如图,用直尺和圆规画出∠ABC的平分线BM,
如图,用直尺和圆规画出∠ABC的平分线BM,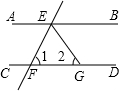 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=