Question

15．解方程或不等式组
（1）解分式方程：$\frac{x}{2x-5}$+$\frac{5}{5-2x}$=1
（2）解不等式组，并把解集在数轴上表示出来．
$\left\{\begin{array}{l}{\frac{x-1}{2}≤\frac{x-4}{3}}\\{4（x+1）＞-10}\end{array}\right.$．

Answer 1

分析 （1）方程两边同乘以最简公分母2x-5，移项、合并同类项、系数化为1，并检验可得；
（2）分别求出每个不等式的解集，再确定其公共部分即可得．

解答 解：（1）去分母，得：x-5=2x-5，
移项，得：x-2x=-5+5，
合并同类项，得：-x=0，
系数化为1，得：x=0，
经检验：x=0是原方程的解；
（2）解不等式组：$\left\{\begin{array}{l}{\frac{x-1}{2}≤\frac{x-4}{3}}&{①}\\{4（x+1）＞-10}&{②}\end{array}\right.$，
解不等式①，得：x≤-5，
解不等式②，得：x＞-$\frac{7}{2}$，
将不等式解集表示在数轴上如下：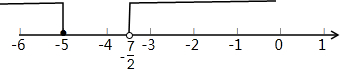

故原不等式组无解．

点评 本题主要考查解分式方程和不等式组的基本能力，严格遵循解方程或不等式的基本步骤是关键．