题目内容
18.如图,在平面直角坐标系中,点A坐标为(-4,0),点B坐标为(0,4),点E为射线BA上的动点(点E不与点A,B重合),抛物线上存在动点T,使得∠EOT=45°,C为y轴正半轴上一点,且OC=$\frac{3}{4}$$\sqrt{2}$AB,抛物线y=-x2+mx+n的图线经过A,C两点.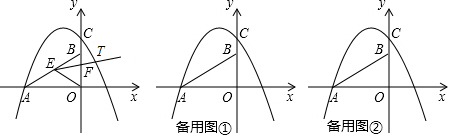
(1)求此抛物线的函数解析式;
(2)若点E的横坐标为-3,求点T的坐标;
(3)抛物线上是否存在点P,使得S△ACP=2S△ABC,若存在,求点P的坐标;若不存在,说明理由.
分析 (1)先求出点C坐标,把A(-4,0)和C(0,6)代入y=-x2+mx+n得$\left\{\begin{array}{l}{n=6}\\{-16-4m+n=0}\end{array}\right.$,解方程组即可.
(2)易知点E坐标(-3,1),作EG⊥OA于G,取点H(1,3),作HM⊥x轴于M,连接EH交抛物线于T,构造等腰直角三角形解决问题.求出直线EH,解方程组求出点T坐标即可.
(3)如图2中,由图象可知点P只有在直线AC下方,设点H(0,2),过点H作AC的平行线交抛物线于P1,P2.首先说明P1,P2满足条件,求出直线P1P2,解方程组即可解决问题.
解答 解:(1)∵点A坐标为(-4,0),点B坐标为(0,4),
∴OA=OB=4,AB=4$\sqrt{2}$,
∴OC=$\frac{3}{4}$$\sqrt{2}$AB=6,
∴C(0,6),
把A(-4,0)和C(0,6)代入y=-x2+mx+n得$\left\{\begin{array}{l}{n=6}\\{-16-4m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{5}{2}}\\{n=6}\end{array}\right.$,
∴抛物线的解析式为y=-x2-$\frac{5}{2}$x+6.
(2)如图1中,
∵A(-4,0),B(0,4),
∴直线AB的解析式为y=x+4,
∴x=-3时,y=1,
∴点E坐标(-3,1),作EG⊥OA于G,取点H(1,3),作HM⊥x轴于M,连接EH交抛物线于T.
∵EG=OM=1,OG=HM=3,∠EGO=∠HMO=90°,
∴△EOG≌△OHM,
∴EO=OH,∠EOG=∠OHM,
∴∠MOH+∠MHO=90°,
∴∠EOG+∠HOM=90°,
∴∠EOH=90°,
∴∠OEH=∠EHO=45°,
∵E(-3,1),H(1,3),
∴直线EH的解析式为y=$\frac{1}{2}$x+$\frac{5}{2}$,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{5}{2}}\\{y=-{x}^{2}-\frac{5}{2}x+6}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{3+\sqrt{23}}{2}}\\{y=\frac{13+\sqrt{23}}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{23}}{2}}\\{y=\frac{13-\sqrt{23}}{4}}\end{array}\right.$,
∵T在第二象限,
∴T($\frac{3+\sqrt{23}}{2}$,$\frac{13+\sqrt{23}}{4}$).
(3)如图2中,由图象可知点P只有在直线AC下方,设点H(0,2),过点H作AC的平行线交抛物线于P1,P2.
∵S△ACH=2S△ABC,
∴${S}_{△{P}_{1}AC}$=${S}_{△{P}_{2}AC}$=2S△ABC,
∵直线AC的解析式为y=$\frac{3}{2}$x+6,
∴直线P1P2的解析式为y=$\frac{3}{2}$x+2,
由$\left\{\begin{array}{l}{y=\frac{3}{2}x+2}\\{y=-{x}^{2}-\frac{5}{2}x+6}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2+2\sqrt{2}}\\{y=-1+3\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2-2\sqrt{2}}\\{y=-1-3\sqrt{2}}\end{array}\right.$,
∴满足条件的点P坐标为(-2+2$\sqrt{2}$,-1+3$\sqrt{2}$)或(-2-2$\sqrt{2}$,-1-3$\sqrt{2}$).
点评 本题考查了二次函数综合题、待定系数法求二次函数解析式、等腰直角三角形的判定与性质、全等三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用思想知识解决问题,学会取特殊点,添加辅助线构造全等三角形,学会构造平行线利用同底等高的三角形面积相等解决问题,属于中考压轴题.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | 三边中线交点 | B. | 三边高的交点 | ||
| C. | 三个顶角的角平分线交点 | D. | 三边的垂直平分线的交点 |
| A. | a>4 | B. | 0<a<4 | C. | a>2 | D. | 0<a<2 |
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
 如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.
如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.