题目内容
9. 如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6.
如图,已知在平行四边形ABCD中,对角线AC与BD交于点O,且BD⊥CD,若AD=13,CD=5,则BO的长度为6.
分析 根据平行四边形性质得出BC=AD=13,BO=$\frac{1}{2}$BD,根据勾股定理求出BD,即可求出BO的长度.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD=5,BO=$\frac{1}{2}$BD,
∵BD⊥CD,
∴∠BDC=90°
∴在Rt△BDC中,由勾股定理得:BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=12,
∴BO=6.
故BO的长度为6.
故答案为:6.
点评 本题考查了勾股定理和平行四边形的性质的应用,注意:平行四边形的对角线互相平分,平行四边形的对边相等.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
14.下列说法中正确的是( )
| A. | 旋转一定会改变图形的形状和大小 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 相等的角是对顶角 |
18.计算:xn+1•xn-1÷(xn)2的结果是( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
19.因式分解2x+x3的正确结果是( )
| A. | 2(x+x3) | B. | x(2+x2) | C. | 2x(1+x) | D. | x(2+x3) |
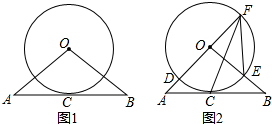
 如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.
如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,试判断四边形AECF是什么样的四边形?写出你的结论并予以证明.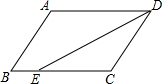 已知,如图在?ABCD中,AD=13,AB=10,DE平分∠ADC交BC于点E,则BE=3.
已知,如图在?ABCD中,AD=13,AB=10,DE平分∠ADC交BC于点E,则BE=3.